Introduction à la complexité algorithmique

Les équations sur cette page sont présentées avec l'aide de MathJax.

Voici une petite introduction (informelle) à la joie du calcul de la complexité algorithmique.

La complexité d'un algorithme est une mesure du temps[1] requis par l'algorithme pour accomplir sa tâche, en fonction de la taille[2] de l'échantillon à traiter.
On dira d'un problème qu'il est aussi complexe que le meilleur algorithme connu pour le résoudre.

Dans certains cas, par exemple celui des algorithmes de tri, on connaît les algorithmes optimaux dans certaines circonstances. Il est en effet possible de démontrer (par l'absurde) dans ces cas qu'il est impossible de faire mieux que le meilleur algorithme connu. Les cas où nous connaissons avec certitude la solution optimale ne sont pas nombreux, cela dit, et il nous reste beaucoup de travail à faire...

Ce texte de Cosmin Negruseri en 2013 met en relief quelques nombres descriptifs de complexité algorithmique, ce qui donne un aperçu des difficultés rencontrées face à certains problèmes et de la taille des échantillons qu'il est chaque fois raisonnable d'essayer de traiter : http://www.infoarena.ro/blog/numbers-everyone-should-know

Calculer la complexité d'un algorithme

Cela peut sembler évident a posteriori, mais voilà : pour calculer la complexité d'un algorithme donné, il convient tout d'abord de compter le nombre d'opérations impliquées par son exécution.

Les exemples donnés ici le sont selon la notation C++, mais l'emploi de pseudocode aurait amplement suffi à la démonstration. La plupart des bouquins d'algorithmique utilisent une notation se rapprochant de celle du langage Pascal.

Notation $O$

La notation la plus utilisée pour noter la complexité d'un algorithme est la notation $O$ (pour ordre de...), qui dénote un ordre de grandeur. Par exemple, on dira d'un algorithme qu'il est $O(15)$ s'il nécessite au plus $15$ opérations (dans le pire cas) pour se compléter. En français, on dira qu'il est $O$ de $15$ ou encore de l'ordre de $15$ .

Souvent, comme dans le cas où un algorithme manipule un tableau de $n$ éléments (on dira un tableau de taille $n$ ), la complexité sera notée en fonction de cette taille. Par exemple, un algorithme de complexité $O(2n+8)$ prendra dans le pire cas huit opérations, plus deux opérations supplémentaires par élément du tableau.

La notation $O$ a le mérite de simplifier très facilement. Nous verrons comment y arriver sous peu.

Algorithmes de complexité constante

Commençons par un exemple simple, soit celui d'une fonction prenant en paramètre le rayon d'une sphère, calculant le volume de cette sphère, et retournant cette valeur au sous-programme appelant. On aura le code proposé à droite.

L'instruction notée (0) est l'affectation d'une valeur à une constante. On peut compter celle-ci comme étant une opération (certains l'omettront, ce qui importe peu, comme nous le verrons plus bas).

L'instruction notée (1) est composée de cinq opérations arithmétiques et d'une affectation. On peut la compter comme six opérations ou comme une seule (ce qui importe peu aussi).

L'instruction notée (2), la production de la valeur résultante de l'exécution de la fonction, est aussi une opération.

double volume_sphere(double rayon) {
   const double PI = 3.14159; // (0)
   double volume;
   volume = 4.0 / 3.0 * PI * rayon * rayon * rayon; // (1)
   return volume; // (2)
}

Si on additionne tout ça, on arrive à deux opérations, si on ne compte pas l'affectation d'une valeur à la constante – opération (0) – et si on compte l'instruction (1) comme une seule opération, et à huit opérations si on compte les instructions de manière plus rigide. L'algorithme sera donc $O(2)$ ou $O(8)$ , tout dépendant de la manière de compter les opérations.

L'important ici n'est pas la valeur exacte entre les parenthèses suivant le $O$ , mais le fait que cette valeur soit constante.

Lorsqu'un algorithme est $O(c)$ où $c$ est une constante, on dit qu'il s'agit alors d'un algorithme en temps constant.

Une complexité constante est la complexité algorithmique idéale, puisque peu importe la taille de l'échantillon à traiter, l'algorithme prendra toujours un nombre fixé à l'avance d'opérations pour réaliser sa tâche.

Tous les algorithmes en temps constant font partie d'une classe nommée $O(1)$ . En général, qu'un algorithme soit $O(3)$ , $O(17)$ ou $O(100000)$ , on dira de lui qu'il est en fait $O(1)$ puisque la différence de performance entre deux algorithmes en temps constant peut être comblée par un simple remplacement matériel (utiliser un processeur plus rapide, par exemple).

On parle parfois de complexité constante amortie, dans le cas d'algorithmes qui prennent un temps constant pour l'essentiel, quitte à coûter un peu plus cher à l'occasion mais de manière telle que ces « hoquets » de l'algorithme s'effacent quand on l'applique sur une séquence suffisamment grande d'éléments. Les algorithmes de complexité constante amortie sont constants « vus de loin » mais peuvent être plus lents que prévus de manière occasionnelle (et posent donc problème dans certains créneaux applicatfis pointus comme celui des systèmes en temps réel).

Le cas classique est la méthode push_back() d'un vecteur en C++, qui s'exécute en temps constant quand la capacité du vecteur dépasse son nombre d'éléments mais implique une réallocation lorsque le nombre d'éléments est égal à la capacité – tant que cette situation ne survient que rarement, l'algorithme s'exécute essentiellement en temps constant.

Pour plus de détails sur l'analyse des algorithmes en temps constant amorti, voir http://mortoray.com/2014/08/11/what-is-amortized-time/ par Edaqa Mortoray en 2014.

Autres exemples $O(1)$

On peut penser au cas (presque trop banal pour être vrai) d'une fonction qui permette d'accéder au $n$ -ème élément d'un tableau. Peu importe la valeur de $n$ , peu importe la taille du tableau, le temps d'accès sera identique[3]. Une version naïve est celle proposée par la fonction obtenir_element_v0() ci-dessous.

template <int N>
   int obtenir_element_v0(const int (&tab)[N], int n) {
      return tab[n];
   }

L'algorithme précédent semble vraiment $O(1)$ (et l'est, à peu de détails près : le passage par un indice implique une addition et une indirection de pointeur). Si on veut rédiger un algorithme qui fait la même tâche tout en validant que l'indice $n$ se trouve entre les bornes minimales et maximales du tableau à accéder, on pourrait avoir, aussi en temps constant, mais $O(5)$ .

const int INDICE_INVALIDE = -1; // arbitraire
template <int N>
   int obtenir_element_v1(const int (&tab)[N], int n) {
      int resultat;
      if (0 <= n && n < N)
         resultat = tab[n];
      else
         resultat = INDICE_INVALIDE;
      return resultat;
   }

Notez que la valeur de la constante INDICE_INVALIDE ne doit pas faire partie des valeurs admises dans le tableau pour que cet algorithme soit correct.

Une autre version, celle-ci de complexité $O(4)$ (donc essentiellement équivalente à l'algorithme précédent, à une affectation près – différence que la compilation fera probablement disparaître) serait obtenir_element_v2().

const int INDICE_INVALIDE = -1; // arbitraire
template <int N>
   int obtenir_element_v2(const int (&tab)[N], int i) {
      return 0 <= i && i < N? tab[i]: INDICE_INVALIDE;
   }

Notez que le recours à une constante interne dans les deux dernières versions est une mauvaise pratique de programmation (après tout, nous voulons que le code client connaisse la valeur de cette constante!) et que ce sont des approches tellement simples qu'on peut à peine les nommer algorithmes.

Cela dit, il existe des algorithmes $O(1)$ de portée beaucoup plus riche et pertinente...

Algorithmes de complexité logarithmique

Non, nous ne calculerons pas de logarithmes ici. N'empêche : la classe de complexité suivante est celle des algorithmes à complexité logarithmique.

Souvent, les algorithmes de ce genre auront la propriété suivante: on leur donne un échantillon de taille $n$ à traiter, et ils font en sorte (dans une répétitive) de diminuer (de moitié, par exemple) à chaque itération[4] la partie de l'échantillon qu'il vaut la peine de traiter. On peut penser, à tout hasard, à une recherche dichotomique.

Exemple de recherche dichotomique

Supposons qu'on nous donne un tableau d'entiers triés (en ordre croissant, pour simplifier). Le fait que le tableau soit trié est important dans ce cas – l'algorithme n'a pas de sens sinon.

#include <iostream>
const int INDICE_INVALIDE = -1;
template <int N>
   int trouver_indice(const int (&tab)[N], int val);
int main() {
   using namespace std;
   int tab[] { // le contenu est trié en ordre croissant
      3, 4, 6, 8, 17, 22, 199, 201, 202
   };
   cout << "L'élément de valeur " << 4 << " se trouve à l'indice "
        << trouver_indice(tab, 4) << endl;
}

Supposons qu'on nous demande à quelle position de ce tableau se trouve un élément d'une valeur bien précise, et que le rôle de notre algorithme soit de retourner l'indice où se trouve ladite valeur – ou de retourner un indicateur d'erreur quelconque si l'élément ne s'y trouve pas.

Pour l'exécution d'un programme comme celui ci-dessus, on pourrait s'attendre à l'affichage suivant :

L'élément de valeur 4 se trouve à l'indice 1

...du fait que la valeur 4 constitue le deuxième élément du tableau tab[], et se trouve conséquemment à la position 1 dans ce tableau.

Solution simple mais inefficace

On peut facilement imaginer la solution simple (mais relativement inefficace) ci-dessous.

template <int N>
   int trouver_indice(const int (&tab)[N], int val) {
      int indice,
          compteur;
      compteur = 0;
      while (compteur < N && tab[compteur] != val)
         ++compteur;
      if (compteur < N) // si la valeur a été trouvée
         indice = compteur;
      else
         indice = INDICE_INVALIDE;
      return indice;
   }

Elle a la qualité d'être simple à rédiger et à comprendre. Elle a toutefois le défaut d'être complexe au sens où nous définissons la complexité algorithmique :

Il y a un certain nombre d'opérations incontournables qui devront toujours être considérées quoiqu'il arrive. On en compte en fait ici quatre, soit – avant la boucle – l'initialisation de la variable compteur, et – après la boucle – la comparaison de compteur avec N, l'affectation d'une valeur à la variable indice, et la production de la valeur de la fonction (énoncé return)
Dans le meilleur cas (sise trouve à l'élémentde), il nous faut seulement $2+4$ opérations pour produire la solution, où le $2$ constitue les deux conditions à évaluer au début de la boucle, et le $4$ est le nombre d'opérations incontournables à faire
Dans le pire cas (sise trouve à l'élémentde, ou si cette valeur n'est pas du tout présente dans), il nous faut par contre $3 \times N + 4$ opérations pour produire la solution (deux comparaisons et une incrémentation de compteur par itération, pour $N$ itérations, donc $3 \times N$ , ce à quoi s'ajoutent les $4$ opérations de base)
Dans le cas moyen qui est ici le plus pertinent, puisqu'en présumant que la fonction pourra être appelée de manière uniforme pour des éléments parfois près du début de, et parfois près de la fin de, il faudra en moyenne $3(\frac{N}{2})+4$ opérations pour produire la solution. Je vous laisse réfléchir à celle-là

Cela signifie qu'en moyenne, cet algorithme nécessitera :

$19$ , donc $3 \times (\frac{10}{2})+4$ , opérations pour un tableau de $10$ éléments
$154$ , donc $3 \times (\frac{100}{2})+4$ , opérations pour un tableau de $100$ éléments
$1504$ , donc $3 \times (\frac{1000}{2})+4$ , opérations pour un tableau de $1000$ éléments
$15004$ , donc $3 \times (\frac{10000}{2})+4$ , opérations pour un tableau de $10000$ éléments

Notez toutefois que dans le pire cas, cet algorithme nécessitera :

$34$ , donc $3 \times 10 + 4$ , opérations pour un tableau de $10$ éléments
$304$ , donc $3 \times 100 + 4$ , opérations pour un tableau de $100$ éléments
$3004$ , donc $3 \times 1000 +4$ , opérations pour un tableau de $1000$ éléments
$30004$ , donc $3 \times 10000 + 4$ , opérations pour un tableau de $10000$ éléments

La croissance de complexité concrète est assez visible[5]. Mais puisque nous voulons ici présenter la complexité logarithmique, nous procéderons avec une meilleure solution – une qui sera moins complexe selon notre définition de la complexité.

La solution de complexité logarithmique

Examinons maintenant une solution plus efficace, et analysons rapidement le nombre d'opérations impliquées (en fonction de $N$ ) :

const int INDICE_INVALIDE = -1;
template <int N>
   int trouver_indice(const int (&tab)[N], int val) {
      //
      // Initialisation
      //
      int ndx = INDICE_INVALIDE;
      int plafond = N - 1;
      int plancher = 0;
      bool trouve = false;
      //
      // Traitement
      //
      while (!trouve && plancher <= plafond) {
         const int MILIEU = (plancher + plafond) / 2; // risqué!
         if (val == tab[MILIEU]) {
            trouve = true;
            ndx = MILIEU;
         } else if (val < tab[MILIEU]) {
            plafond = MILIEU - 1;
         } else { // val > tab[MILIEU]
            plancher = MILIEU + 1;
         }
      }
      //
      // Production du résultat
      //
      return ndx;
   }

On y compte quatre opérations avant le coeur du traitement, et une autre tout juste après, ce qui fait en sorte que nous ayons cinq opérations à faire, quoi qu'il arrive.

Le traitement en tant que tel peut se décomposer comme suit :

Deux opérations dans le teste de la condition de poursuite de la boucle
Trois opérations si, à l'intérieur de la boucle, le premier test de condition est un succès (si on entre dans le if)
Trois opérations si, à l'intérieur de la boucle, le premier test de condition échoue mais le second est un succès (si on entre dans le else if), et
Trois opérations si, à l'intérieur de la boucle, le premier test de condition échoue et qu'il en va de même pour le second (si on entre dans le else)

Quoiqu'il arrive, on devra répéter $2+3$ , donc cinq opérations un certain nombre de fois. La grande question ici est : combien de fois?

Nous n'entrerons pas dans les calculs – pas qu'ils soient inintéressants, mais simplement parce qu'ils sont un peu plus mathématiques que ce que ce cours est en droit de viser – sinon pour faire remarquer qu'à chaque itération, il peut se produire une de trois choses suivantes :

Ou on trouve la valeur recherchée (cas du if), ce qui complète la tâche
Ou on réduit la taille de l'échantillon de moitié pour n'en explorer que la moitié inférieure, ayant convenu que la valeur recherchée ne peut pas se trouve au-dessus (cas du else if)
Ou on réduit la taille de l'échantillon de moitié pour n'en explorer que la moitié supérieure, ayant convenu que la valeur recherchée ne peut pas se trouve en-dessous (cas du else)

Le pire cas est donc d'éliminer successivement la moitié des éléments restant à explorer jusqu'à ce qu'il n'en reste plus qu'un seul, qui sera alors le bon ou encore qui indiquera que l'élément cherché est absent du tableau. Analysons un peu plus ce pire cas :

Si on explore un tableau de $10$ éléments, on aura besoin au pire de $4$ itérations. L'espace à explorer sera initialement de $10$ éléments, puis de $5$ éléments, puis $2$ , puis d'un seul
Si on explore un tableau de $100$ éléments, on aura besoin au pire de $7$ itérations. L'espace à explorer sera initialement de $100$ éléments, puis de $50$ éléments, puis $25$ , puis $12$ , puis $6$ , puisà $3$ , puis d'un seul
Si on explore un tableau de $1000$ éléments, on aura besoin au pire de $10$ itérations. L'espace à explorer sera initialement de $1000$ éléments, puis de $500$ éléments, puis $250$ , puis $125$ , puis $62$ , puis $31$ , puis $15$ , puis $7$ , puis $3$ , puis d'un seul

Vous pouvez vous amuser à calculer d'autres valeurs. L'équation générale dit que cet algorithme est de complexité $O(b+(i \times \log_2{n}))$ où $n$ est la taille du tableau (exprimée en nombre d'éléments), $b$ est le nombre incontournable d'opérations (ici, $b=5$ ) et $i$ est la complexité d'une seule itération (ici, $i=5$ aussi, mais c'est accidentel).

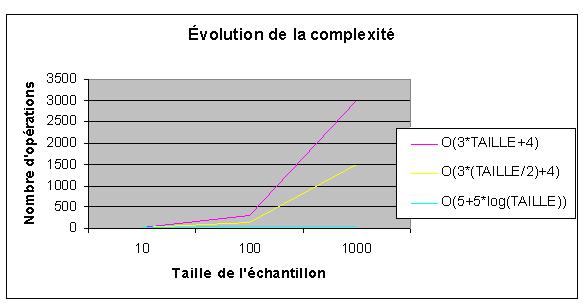
Le tableau suivant présente les le nombre d'opérations requis selon la complexité, pour différentes tailles de tableaux.

$N$	$O(3 \times N + 4)$	$O(3 \times \frac{N}{2} + 4)$	$O(5 + 5 \times \log_2 N + 4)$
$10$	$34$	$19$	$25$
$100$	$304$	$154$	$40$
$1000$	$3004$	$1504$	$55$
$10000$	$30004$	$15004$	$75$
$100000$	$300004$	$150004$	$90$
$1000000$	$3000004$	$1500004$	$105$

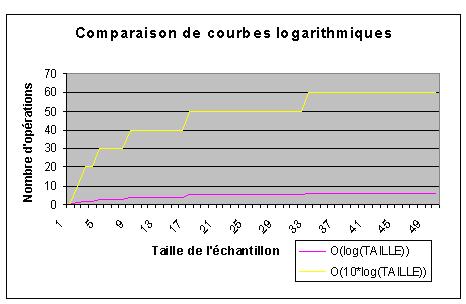
Ce qu'il faut retenir ici, c'est l'évolution de la complexité. Simplement en traçant la courbe des valeurs calculés pour certaines tailles choisies d'échantillons, on peut souvent voir s'il s'agit ou non d'une complexité logarithmique.

Remarquez que la courbe de l'algorithme logarithmique est tellement peu accentuée par rapport aux deux autres qu'on la voit à peine sur le graphique (et encore : celui-ci ne présente que des valeurs propres à des tailles de tableau allant jusqu'à $1000$ , ce qui est bien petit en informatique.

L'avantage de la solution de complexité logarithmique sur les deux autres est très net. En fait, si on avait ajouté au graphique les échantillons plus grands, la courbe logarithmique serait à toutes fins pratiques disparue de notre champ de vision, la croissance des autres dans ce graphique étant vertigineuses en comparaison avec elle.

On peut améliorer légèrement l'algorithme de complexité logarithmique en ajoutant quelques variables temporaires. C'est une optimisation locale, mais qui peut le rendre encore un petit peu plus efficace.

On aurait alors :

const int INDICE_INVALIDE = -1;
template <int N>
   int trouver_indice(const int tab[], int N, int val) {
      //
      // Initialisation
      //
      int ndx = INDICE_INVALIDE;
      int plafond = TAILLE - 1;
      int plancher = 0;
      bool trouve = false;
      //
      // Traitement
      //
      while (!trouve && plancher <= plafond) {
         // pour optimiser le traitement dans la boucle
         const int ndx_cur= (plancher + plafond) / 2; // risqué!
         const int val_cur = tab[ndx_cur];
         if (val == val_cur) {
            trouve = true;
            ndx = ndx_cur;
         } else if (val < val_cur) {
            plafond = ndx_cur - 1;
         } else { // val > val_cur
            plancher = ndx_cur + 1;
         }
      }
      return ndx;
   }

Questions de notation

Nous avons écrit plus haut que notre algorithme était de complexité $O(5+5 \times n)$ . On trouve donc, dans le calcul de sa complexité, une addition, une multiplication, et un calcul de logarithme.

Pourquoi dit-on alors qu'il s'agit là d'une complexité logarithmique?

Le raisonnement est le suivant :

D'abord, l'addition d'une constante à la complexité est un détail inconséquent sur sa complexité réelle. Plus la taille de l'échantillon à traiter croît, moins l'addition d'une constante à la complexité de l'algorithme devient importante. Ainsi, on simplifiera la complexité $O(5+5 \times \log_2 n)$ pour obtenir $O(5 \times \log_2 n))$
Ensuite, la multiplication par une constante a elle aussi de moins en moins d'importance sur la complexité réelle de l'algorithme si on regarde son poids relatif sur des échantillons de grande taille. Ainsi, à moins de faire des optimisations très pointues, on dira souvent que la complexité $O(5 \times \log_2 n)$ est équivalente à $O(\log_2 n)$ . Ceci est moins évident dans le graphique précédent, mais devient visible sur de grandes valeurs de $n$
Ainsi, notre algorithme, vu de façon générale, entre dans la grande classe des algorithmes de complexité logarithmique

Algorithmes de complexité linéaire

Nous avons déjà vu un algorithme de complexité linéaire un peu plus haut.

Par complexité linéaire, ou $O(n)$ , on dénotera des algorithmes pour lesquels le nombre d'étapes à effectuer variera en proportion directe de la taille de l'échantillon à traiter : si l'échantillon croît par un facteur de $100$ , la complexité sera accrue elle aussi par un facteur de $100$ .

Pensez à un algorithme qui parcourt chaque élément d'une liste chaînée, ou qui fait la somme des éléments d'un tableau (ici $O(3+n \times 5)$ )...

template <int N>
   int somme_elements(const int (&tab)[N]) {
      int somme = 0;
      for (int compteur = 0; compteur < N; ++compteur)
         somme += tab[compteur]; // attention aux débordements!
      return somme;
   }

...ce qui donnerait, avec une liste chaînée ( $O(2 + n \times 5)$ )...

int somme_elements(const Noeud *p) {
   int somme = 0;
   while (p) {
      somme += p->valeur; // mettons; attention aux débordements!
      p = p->successeur;
   }
   return somme;
}

La simplification normale s'applique : on élimine l'addition de constantes, puis la multiplication par des constantes, pour réaliser que la croissance de la complexité dépend directement de la taille de l'échantillon. Il s'agit de la donnée intéressante du calcul.

If you don't know what $O(N^2)$ means, think how long it takes to sing the $N$ days of Christmas – John D. Cook (source)

Algorithmes de complexité quadratique

On dira d'un algorithme de complexité $O(n^2)$ qu'il est de complexité quadratique. Vous comprenez sûrement le principe du calcul de la complexité maintenant, alors nous n'entrerons pas ici dans les détails.

Nous n'irons pas plus loin dans notre description en surface de la complexité algorithmique. Notons seulement qu'il existe plusieurs autres niveaux de complexité (par exemple, des complexités comme $O(n^3)$ , $O(n^4)$ , ou des complexités mettant en relation plusieurs variables comme $O(n+m^2)$ ).

Ce qui est vraiment à retenir ici est qu'il est possible de calculer la complexité d'un algorithme, et de comparer la complexité relative de deux algorithmes pour choisir le plus efficace. Certains algorithmes en apparence simples sont extrêmement lents; il convient donc de choisir nos solutions avec prudence.

Exemple d'algorithme à complexité quadratique : un algorithme de tri à bulles, comme dans le programme à droite, qui met en ordre de manière inefficace les éléments d'un tableau.

Cet algorithme proposé est de complexité $O((2+n) \times (2+n))$ dans le meilleur cas, et $O((2+n) \times (5+n))$ dans le pire cas; on parle donc après simplification d'un algorithme $O(n \times n)$ , ou plus simplement $O(n^2)$ .

En terminant, il existe des horreurs algorithmiques (dites « non polynomiales », dont la complexité ne s'exprime pas sous la forme d'un polynôme) qu'il faut éviter si on en a le choix. On parle par exemple d'algorithmes de complexité $O(2^n)$ . Vous pouvez vous amuser à tracer la courbe dénotant le nombre d'opérations pour ce genre d'algorithme... ça fait carrément peur! Pour en savoir plus, lisez ce petit texte.

void permuter(int &a, int &b) {
   int temp = a;
   a = b;
   b = temp;
}
template <int N>
   void tri_bulle(int (&tab)[N]) {
      for (int i = 0; i < N; i++)
         for (int j = i+ 1; j < N; j++)
            if (tab[i] > tab[j])
               echanger(tab[i], tab[j]);
   }

Lectures complémentaires

Quelques liens pour enrichir le propos.

Pour une discussion intéressante de l'importance de la complexité algorithmique dans l'algorithmique en général et dans la programmation générique en particulier, voir cette entrevue avec Alexander Stepanov, concepteur de la bibliothèque STL.
Une Cheat Sheet de la complexité algorithmique associée à plusieurs structures de données et algorithmes connus : http://bigocheatsheet.com/
Voir aussi ce chouette texte comparant diverses stratégies pour résoudre un problème a priori simple à l'aide d'outils de la bibliothèque standard de C++.
Explication de ce qu'est la complexité algorithmique, par Justin Abrahams (qui se présente lui-même comme un programmeur autodidacte) en 2013 : http://justin.abrah.ms/computer-science/big-o-notation-explained.html
Présentation de la notation « grand O » et de ses ramifications pratiques pour les programmeuses et les programmeurs, par Roger Orr (un très sympathique monsieur) en 2014 : http://accu.org/content/conf2014/Order_Notation_in_Practice.pdf
Introduction à la complexité algorithmique et à la notation qu'on y utilise, par Mike James en 2015 : http://www.i-programmer.info/babbages-bag/499-computational-complexity.html
À propos des classes de complexité, texte de R .J. Lipton en 2010 : https://rjlipton.wordpress.com/2010/11/07/what-is-a-complexity-class/
En 2016, Peter Norvig discute du nombre relativement petit d'atomes dans l'univers, et compare ce nombre avec la complexité de certains problèmes : http://norvig.com/atoms.html
Dans cette présentation de 2016, Andrei Alexandrescu donne entre autres un aperçu de l'inférence de complexité algorithmique en D, un mécanisme particulièrement utile dans le cas de code générique : http://fr.slideshare.net/AndreiAlexandrescu2/dconf-2016-opening-keynote
Texte depar Sergey Ignatchenko, qui epxlique que certains « $O$ » sont plus gros que d'autres, surtout quand on tient compte de l'effet de la Cache : http://ithare.com/some-big-os-are-bigger-than-others/

[1] Le terme temps doit être pris ici au sens de nombre d'étapes requis pour arriver à une solution – on parle donc d'un temps discret, pas continu. On peut examiner le temps requis pour exécuter un algorithme donné dans le meilleur cas possible, dans le pire cas possible, et dans le cas moyen.

[2] Le terme taille doit être pris ici au sens de nombre d'éléments dans l'échantillon à traiter par l'algorithme. Souvent, on utilisera un tableau contenant un nombre donné d'éléments ou une chaîne de caractères dont on peut connaître le nombre de caractères constitutifs comme échantillon à traiter, pour faciliter les calculs.

[3] En serait-il autant d'une fonction accédant au i-ème élément d'une liste chaînée?

[4] Une itération est un tour de boucle.

[5] Nous verrons plus loin qu'il s'agit là d'un algorithme de complexité linéaire ( $O(n)$ ), où $n$ est la taille du tableau).