
Les équations sur ce site sont affichées avec MathJax.
Pour les intéressé(e)s : sur Wikipedia, un débat fait rage à savoir quelle place donner aux preuves dans une telle encyclopédie.
La preuve, mise en relief par la démonstration, est sans doute le propos principal de l'acte mathématique, ce sur quoi repose sa rigueur. S'il y a un sujet au coeur des mathématiques, c'est probablement celui-ci.
Le mot « preuve » a plusieurs sens, mais son sens scientifique est pointu et, dans son acception mathématique, l'est encore plus.
L'acte scientifique tout entier repose sur la preuve. La science implique à la fois le doute et le devoir de démontrer ce qui est avancé de manière à ce que d'autres puissent reprendre la même démarche et valider (ou invalider) les résultats. C'est d'ailleurs l'essence par laquelle il est légitime de refuser la proposition faite par certain(e)s selon lesquel(le)s la science est une religion – en fait, si la science dépend d'une chose, c'est du doute et de sa propre remise en question, sans quoi elle n'est tout simplement pas.
C'est vrai pour la science empirique, évidemment, mais encore plus pour la mathématique, où une preuve n'est admise que jusqu'à preuve (!) du contraire, et suite à une étude approfondie de l'argumentaire par les pairs. Si une faute logique est trouvée, ce qui arrive très souvent, alors il faut se remettre à l'ouvrage. La science est, par nature, une oeuvre communautaire : affirmer sans démontrer ou soumettre au regard de l'autre est un comportement qui échappe à son domaine.
Les techniques plus traditionnelles de preuve comme la preuve directe, l'induction, la contradiction (qui n'est pas admise par certaines écoles de pensée comme l'intuitionnisme), la contraposition ou, au centre d'éléments marquants de l'histoire de l'informatique, la diagonalisation, etc. font partie du cursus scientifique d'à peu près tout le monde. L'informatique permet de nouvelles formes de preuve, comme par exemple la preuve par exhaustion (couvrir tous les cas possibles), qui rendent la vérification par les pairs difficile (les problèmes sont trop gros et les preuves très fastidieuses; c'est pourquoi on utilise des programmes!). La preuve par exhaustion a permis de démontrer la conjecture de Kepler... du moins aux yeux de celles et ceux qui admettent cette technique de preuve comme légitime.
Ces changements demandent à tous les scientifiques de se questionner sur la nature de la vérification des preuves, une question fondamentale. En effet, si on utilise un programme pour démontrer la validité de la preuve faite par un autre programme, alors il faudra s'assurer que ce nouveau programme est correct... Mais est-on certain que la revue par les pairs, plus traditionnelle, est plus correcte?
La démonstration de la validité des programmes et la preuve assistée sont deux sujets au coeur d'un certain nombre d'avancées fondamentales en informatique, incluant le développement des langages ALGOL et Lisp, et l'idée même de la machine de Turing.
La science est questionnement et doute. La rigueur du raisonnement y est fondamentale.
Quelques liens d'ordre général sur le sujet :
Textes de nature historique :
Les liens entre la preuve et la programmation sont plus nombreux que l'on pourrait le croire a priori. À ce sujet :
Les preuves expliquées aux programmeuses et aux programmeurs, par Jeremy Kun en 2013 :
À quoi ressemble une preuve? Existe-t-il des preuves particulièrement célèbres? Ce qui suit n'est absolument pas exhaustif, évidemment...
Il ne faut pas confondre la preuve mathématique par induction et le raisonnement inductif, qui, habituellement pris par opposition au raisonnement déductif, a un sens précis mais différent et est surtout utilisé en philosophie. En effet, un raisonnement inductif a comme particularité que la véracité de ses prémisses rend probable sa conclusion; un raisonnement déductif a comme particularité que la véracité de ses prémisses est supposé garantir la véracité de sa conclusion.
Le site http://www.jps.at/philosophy/dednindn.html suggère d'ailleurs une définition probabiliste de la véracité d'une proposition étant donné des prémisses vraies pour les termes :
J'insérerai ici des petits trucs quant à certaines techniques de preuve, en fonction du temps que j'aurai à ma disposition.
Technique développée par Georg Cantor pour attaquer certains problèmes ayant trait à l'infini.
À ce sujet :
Dans une preuve par induction, on vise à démontrer la véracité d'un énoncé pour les éléments d'un ensemble donné. Pour ce faire, on démontre formellement la propriété pour un cas choisi avec soin (la base de l'induction), puis on montre que si la propriété tient pour un élément donné (ce qui est l'hypothèse de l'induction), alors elle tient aussi pour l'élément suivant (ce qui est le pas de l'induction, et constitue ce qui doit être démontré).
Les preuves par induction sont particulièrement utiles pour démontrer des théorèmes sur des ensembles dénombrables, comme l'ensemble des entiers naturels, et pour démontrer des énoncés ayant trait à la longueur d'une séquence (par exemple celle d'une chaîne de caractères).
Quelques liens :

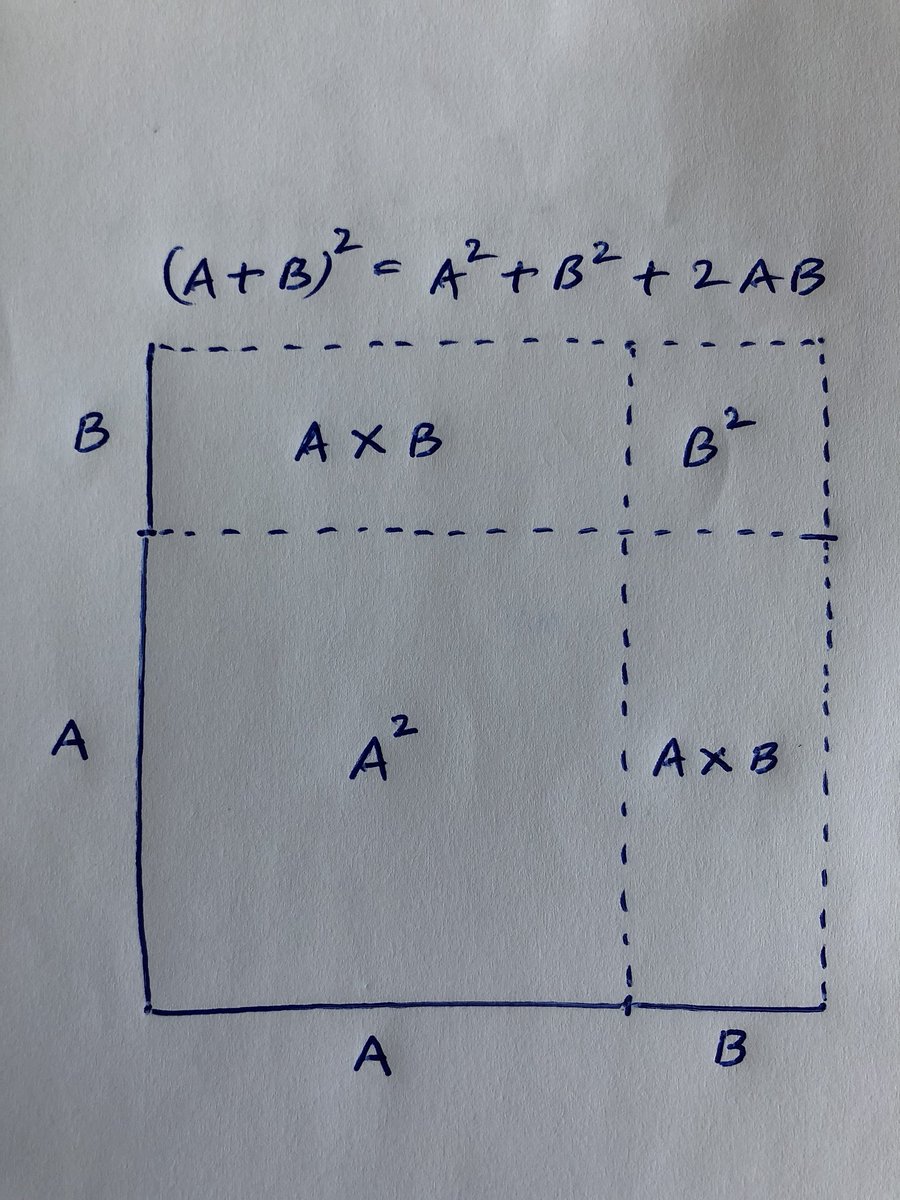
Bien qu'elles ne soient pas considérées comme suffisamment rigoureuses pour mériter le titre de « preuve » par certain(e)s, il existe une longue histoire de démonstrations et de preuves reposant sur une visualisation géométrique des concepts exprimés et des relations décrites.
Deux propositions pour démontrer que |
 |
 |