Introduction aux conteneurs et aux itérateurs
Il arrive très fréquemment qu'il soit
nécessaire d'entreposer des éléments de manière
à optimiser certaines opérations (insertion au début,
à la fin ou à un endroit quelconque; suppression d'un élément;
accès à un élément; etc.).
|
Pour réaliser l'entreposage d'objets[1],
on aura recours à divers types de conteneurs.
Un conteneur
permet l'entreposage d'objets et expose, dans la mesure où le
conteneur a la sophistication requise pour ce faire, des méthodes pour
réaliser les opérations usuelles comme par exemple l'insertion
d'un élément, la suppression d'un élément et l'obtention
du nombre d'éléments qui y sont entreposés.
|
La conception de conteneurs
fait habituellement partie de ce qui est enseigné dans un cours
de structures de données. Parmi les conteneurs les plus connus,
on trouve la pile, la file, de même que les listes simplement
et doublement chaînées.
Ici, nous mettrons l'accent non pas sur la conception de
conteneurs mais bien leur formalisation et leur utilisation raisonnée.
|
|
L'opération la plus fondamentale sur une séquence entreposée
dans un conteneur est de la parcourir. Pour parcourir les éléments
d'une séquence, on privilégiera l'emploi d'un itérateur.
Un itérateur
est un objet représentant l'abstraction du concept de séquence.
À l'aide
d'un itérateur, il sera possible à la fois de procéder
d'un élément à l'autre dans une séquence
et d'obtenir la valeur de l'élément vers lequel
mène l'itérateur.
Nous examinerons
plus loin en quoi le concept d'itérateur permet le développement
d'algorithmes extrêmement efficaces et capables d'opérer
sur une vaste variété de conteneurs, ce qui permet aux
développeurs de séparer le concept d'entreposage,
celui de séquence d'éléments entreposés
et celui d'opération sur les éléments d'une
séquence.
|
L'itérateur
est un concept plus fondamental que l'indice.
L'idée d'indice présume (d'un point de
vue pragmatique) la capacité, dans un conteneur, d'atteindre
le i-ème élément
de manière efficace, La jonction des idées de lieu et
de séquence est indépendante d'une telle présomption
et ne compte que sur la capacité, intrinsèque à
toute séquence, d'être navigable. |
Conteneur primitif – le tableau
|
Un tableau brut, en C++,
est une séquence contiguë en mémoire d'éléments
du même type.
L'accès à un élément d'un tableau peut donc se
faire en temps constant à l'aide d'une simple arithmétique
de pointeurs: le ième élément
d'un tableau tab de type T s'exprime tab[i], ce qui est un simple
raccourci pour *(tab+i) ou, de manière
plus verbeuse, ce qui se trouve à l'adresse tab à laquelle on aurait additionné i *
sizeof(T) bytes.
Dans l'exemple proposé à droite :
- La variable tab0 est en mémoire statique, et est un tableau de quatre
éléments
- La variable tab est en mémoire statique, et contient les éléments
1,2,3,8,0,0,...,0 dans l'ordre, donc les éléments aux indices 4
à 9 inclusivement sont initialisés à zéro. Les éléments de tab
sont const, et
ne peuvent donc pas être modifiés une fois construits
- La variable tabz est en mémoire statique,
et contient NELEMS éléments, tous initialisés à
zéro
- La variable tab2 est sur la pile, et
contient N éléments a priori
non-initialisés
- La variable tab3 pointe sur un tableau
alloué dynamiquement de N instances de std::string, toutes vides a priori, car std::string est une classe, et son constructeur par défaut sera
implicitement appelé pour chaque élément
|
#include <string>
#include <memory>
using namespace std;
const int NELEMS = 10;
static int tab0[] { 1, 2, 3, 8 };
const int tab[NELEMS] { 1, 2, 3, 8 };
int tabz[NELEMS] {};
int main() {
const int N = 5;
float tab2[N];
for (int i = 0; i < N; ++i)
tab2[i] = static_cast<float>(i)+0.5f;
// équivalent
for (float *p = tab2+0; p != tab2+N; ++p)
*p = (static_cast<float>(p-tab2) + 0.5f);
// allocation dynamique de N instances de string
unique_ptr<string[]> tab3 { new string[N] };
for (int i = 0; i < N; ++i)
tab3[i] += static_cast<char>('A'+ i);
}
|
La taille d'un tableau situé en mémoire statique ou sur la pile
doit être une constante entière strictement positive, donc dans
l'intervalle , et dont la valeur est connue
à la compilation. La taille d'un tableau alloué sur le tas à
l'aide de mécanismes d'allocation dynamique de mémoire doit être
une valeur entière et positive, donc dans l'intervalle , et peut ne pas être connue à la compilation.
Les tableaux sont peu flexibles mais de constitution très
simple. Le tableau est une structure de données primitive mais essentielle
à la construction d'autres structures plus sophistiquées
et dont la capacité d'autodescription est plus grande, comme les
vecteurs et la plupart des chaînes de caractères à vocation
commerciale.
|
Les problèmes de fond avec les tableaux sont inhérents à
leur constitution :
- Un tableau n'est ni plus ni moins que l'adresse du premier élément
d'une séquence contiguë en mémoire d'éléments
du même type. Le tableau ne contient donc a priori pas
d'information sur sa propre taille – aucune métadonnée
- Un tableau a une taille fixe de sa construction à sa destruction. Si le
besoin se fait sentir de faire croître l'espace de stockage que représente un
tableau, alors il faut avoir recours à de l'allocation dynamique de mémoire et
à un peu de programmation
|
int n;
// ...
unique_ptr<int[]> tab{ new int[n] };
// ... éventuellement, on veut doubler
// la taille de tab
{
// restreindre la portée de p
unique_ptr<int[]> p{ new int[n*2] };
for (int i = 0; i < n; ++i)
p[i] = tab[i];
tab = std::move(p);
}
|
Application simple – une chaîne Pascal
Une application simple d'un tableau de taille fixe dans un conteneur plus spécialisé
serait celui d'une classe représentant une chaîne du langage Pascal.
Les chaînes du langage Pascal
sont de capacité fixe (255 caractères
au maximum) et n'ont pas de délimiteur de fin. La taille (au sens du
nombre d'éléments) de la chaîne est entreposée dans
le premier élément du tableau contenant aussi le texte, ce qui
explique le traitement de ce byte en tant qu'un unsigned char plutôt qu'en tant qu'un char.
L'exemple ci-dessous montre qu'il est possible de construire des conteneurs
efficaces et relativement sécuritaires autour d'un tableau plus primitif,
et ce sans effort excessif. Les opérateurs [] sont
publics et valident les bornes, qui – selon les idiomes Pascal
– sont situés dans l'intervalle pour
une chaîne de taille , plutôt que dans
l'intervalle comme en C
ou en C++.
La taille est toujours immédiatement disponible et est toujours tenue
à jour.
Le code suit. Remarquez que les méthodes publiques utilisent des entiers
signés comme type pour les indices dans une chaîne, dans le but
de réduire les risques de boucle infinie dans le code utilisateur de
ce type. La Sainte-Trinité y est implicitement correcte.
class chaine_pascal {
public:
using size_type = short;
using value_type = char;
private:
enum { MAX = 255 };
value_type texte[MAX + 1]{};
bool indice_legal(size_type n) const noexcept {
return 1 <= n && n < taille();
}
unsigned char& taille() noexcept {
return static_cast<unsigned char&>(texte[0]);
}
unsigned char taille() const noexcept {
return static_cast<unsigned char>(texte[0]);
}
public:
chaine_pascal() = default; // notez que texte[0] == '\0'
chaine_pascal(const char *s) noexcept {
size_type n = {};
while (*s && n < MAX)
texte[++n] = *s++;
taille() = n;
}
size_type size() const noexcept {
return taille();
}
class HorsBornes {};
value_type operator[](size_type n) const {
// if (!indice_legal(n)) throw HorsBornes{}; // si vous y tenez
return texte[n];
}
value_type& operator[](size_type n) {
// if (!indice_legal(n)) throw HorsBornes{}; // si vous y tenez
return texte[n];
}
};
#include <iostream>
using namespace std;
ostream &operator<<(ostream &os, const chaine_pascal &c) {
for (chaine_pascal::size_type i = 1; i <= c.size(); ++i)
os << c[i];
return os;
}
int main() {
chaine_pascal c = "Allo!";
cout << c;
}
Exercice : ajoutez à cette classe les opérateurs
relationnels que sont ==, !=,
<, <=, > et
>=, de même qu'une méthode pour vider la chaîne,
une autre pour concaténer deux chaînes, sous ses déclinaisons
+ et +=, et une autre pour ajouter un élément
en fin de chaîne.
Concept d'itérateur au sens primitif – le pointeur
Un itérateur est une abstraction du concept de séquence. En ce
sens, un itérateur permet à la fois d'accéder à
un élément d'une séquence, d'aller à l'élément
suivant dans une séquence (souvent même d'aller à l'élément
précédent de la séquence), et de tester l'atteinte du début
ou de la fin d'une séquence. Certains itérateurs offrent plus
de services, mais ce sont sans doute là les services les plus élémentaires.
|
En C++,
l'itérateur respecte la notation applicable à un pointeur dans
un tableau, Ainsi, si tab est une séquence
de N éléments de type T, alors :
- Le début de la séquence est tab,
et son type est T*. Notez que sur certains compilateurs
plus stricts, on exigera d'écrire tab+0 pour
provoquer une décrépitude de pointeur et faire passer le type
de l'expression de « tableau de N éléments
du type T » à « pointeur
sur un T », ce qui est le type de la fin de
la séquence (puce suivante)
- La fin de la séquence est tab + N,
aussi de type T*. Par convention (et par souci
d'efficacité), la fin d'une séquence est le premier élément
juste après le dernier élément valide, ce qui explique
que tab + N, pas
tab + N - 1, soit la fin de la séquence. On peut
comparer un itérateur avec la fin de sa séquence, mais on ne peut pas accéder
à l'élément qui s'y trouve, même en lecture
- Un itérateur sur cette séquence sera de type
T*
- Si p est un itérateur sur cette séquence,
alors *p sera le contenu de l'élément
auquel réfère p, appliquer l'opérateur
++ sur p amènera p au prochain élément de la séquence, et lui appliquer
l'opérateur -- amènera p à l'élément précédent dans la séquence
|
T tab[N];
for (auto p = tab+0; p != tab+N; ++p) {
// agir sur *p
}
auto p = tab+N;
// illégal: p est hors séquence
T val = *p;
|
Détection standard des extrémités
Depuis C++ 11,
il existe dans
<iterator> des fonctions très
utiles nommées
std::begin() et
std::end(). Ces fonctions sont en mesure de représenter le début
et la fin d'une séquence standard, dans un tableau comme dans un conteneur
plus sophistiqué, dans la mesure où les dimensions du tableau
sont connues du compilateur au point où ces fonctions sont appelées
(ce qui n'est par exemple pas le cas si le tableau est alloué dynamiquement).
Ainsi, plutôt que d'écrire ceci :
int main() {
const int N = 100;
int vals[N];
for(auto p = vals + 0; p != vals + N; ++p)
*p = 3;
}
... on écrira désormais cela :
#include <algorithm>
int main() {
using namespace std;
const int N = 100;
int vals[N];
for(auto p = begin(vals); p != end(vals); ++p)
*p = 3;
}
... ou encore, pour exactement le même effet :
#include <algorithm>
int main() {
using namespace std;
const int N = 100;
int vals[N];
for(auto & val : vals) // pour chaque référence val sur un élément de vals (génère le même code que ci-dessus)
val = 3;
}
...ce qui est tout aussi efficace mais beaucoup plus élégant et,
surtout, beaucoup plus général. Évidemment, on peut faire
mieux à l'aide d'algorithmes standards...
Exemples d'utilisation d'un tableau
Remplir un tableau de type T d'éléments de même valeur.
|
À l'aide d'indices
|
À l'aide d'indices
(mieux!) |
À l'aide d'un itérateur
|
template <class T>
void init_tableau(T tab[], int n, const T &val) {
for (int i = 0; i < n; ++i)
tab[i] = val;
}
#include <string>
int main() {
using namespace std;
const int N = 100;
int tab0[N];
string tab1[N];
init_tableau(tab0, N, -1);
init_tableau(tab1, N, "test"s);
}
|
template <class T, int N>
void init_tableau(T (&tab)[N], const T &val) {
for (int i = 0; i < N; ++i)
tab[i] = val;
}
#include <string>
int main() {
using namespace std;
const int N = 100;
int tab0[N];
string tab1[N];
init_tableau(tab0, -1);
init_tableau(tab1, "test"s);
}
|
template <class It, class T>
void init_sequence(It debut, It fin, const T &val) {
for (; debut != fin; ++debut)
*debut = val;
}
#include <iterator>
#include <string>
int main() {
using namespace std;
const int N = 100;
int tab0[N];
string tab1[N];
init_sequence(begin(tab0), end(tab0), -1);
init_sequence(begin(tab1), end(tab1), "test"s);
}
|
Trouver la position d'un
élément e dans
un tableau de type T.
| À
l'aide d'indices |
À
l'aide d'indices (mieux!) |
À
l'aide d'un itérateur |
template <class T>
int chercher(const T tab[], int n, const T &e) {
for (int i = 0; i < n; ++i)
if (tab[i] == e) return i;
return -1;
}
#include <iostream>
int main() {
using namespace std;
const int N = 100;
int tab[N];
// ...
if(int val; cin >> val)
if (int ndx = chercher(tab, N, val); ndx != -1)
cout << ndx << endl;
}
|
template <class T, int N>
int chercher(const T (&tab)[N], const T &e) {
for (int i = 0; i < N; ++i)
if (tab[i] == e) return i;
return -1;
}
#include <iostream>
int main() {
using namespace std;
const int N = 100;
int tab[N];
// ...
if(int val; cin >> val)
if (int ndx = chercher(tab, N, val); ndx != -1)
cout << ndx << endl;
}
|
template <class It, class T>
It chercher(It debut, It fin, const T &e) {
for (; debut != fin; ++debut)
if (*debut == e) return debut;
return fin;
}
#include <iterator>
#include <iostream>
int main() {
using namespace std;
const int N = 100;
int tab[N];
// ...
if(int val; cin >> val)
if (auto p = chercher(begin(tab), end(tab), val); p != end(tab))
cout << static_cast<int>(p - tab) << endl;
}
|
Inverser l'ordre des éléments d'un tableau
de type T.
| À
l'aide d'indices |
À
l'aide d'indices (mieux!) |
À
l'aide d'un itérateur |
#include <algorithm>
template <class T>
void inverser(T Tab[], int n) {
using std::swap;
for (int i = 0; i < n/2; ++i)
swap(tab[i], tab[n-i-1]);
}
int main() {
const int N = 100;
int tab[N];
// ...
inverser(tab, N);
}
|
#include <algorithm>
template <class T, int N>
void inverser(T (&tab)[N]) {
using std::swap;
for (int i = 0; i < N/2; ++i)
swap(tab[i], tab[N-i-1]);
}
int main() {
const int N = 100;
int tab[N];
// ...
inverser(tab, N);
}
|
#include <algorithm>
template <class It>
void inverser(It debut, It fin) {
using std::swap;
while(debut != fin) {
--fin;
if (debut == fin) return;
swap(*debut, *fin);
++debut;
}
}
int main() {
using namespace std;
const int N = 100;
int tab[N];
// ...
inverser(begin(tab), end(tab));
}
|
Application simple – une chaîne Pascal
avec itérateurs
Reprenons maintenant la classe
chaine_pascal ci-dessus et ajoutons lui des itérateurs,
déclinés sous forme constante et non constante. Remarquez à
quel point cet ajout est simple et efficace, surtout en comparaison avec les
gains potentiels résultant de la capacité subséquente
d'appliquer plusieurs algorithmes standards sur ce type.
#include <algorithm>
class chaine_pascal {
public:
using size_type = short;
using value_type = char;
private:
enum { MAX = 255 };
value_type texte[MAX + 1]{};
bool indice_legal(size_type n) const noexcept {
return 1 <= n && n < taille();
}
unsigned char& taille() noexcept {
return static_cast<unsigned char&>(texte[0]);
}
unsigned char taille() const noexcept {
return static_cast<unsigned char>(texte[0]);
}
public:
// Itérateurs
using iterator = value_type*;
using const_iterator = const value_type*;
iterator begin() noexcept {
return &texte[1];
}
const_iterator begin() const noexcept {
return &texte[1];
}
iterator end() noexcept {
return begin() + size();
}
const_iterator end() const noexcept {
return begin() + size();
}
chaine_pascal () = default; // notez que texte[0] == '\0'
chaine_pascal(const char *s) noexcept {
auto it = begin();
while (*s && it < begin()+MAX) *++it = *s++;
taille() = static_cast<size_type>(it - begin());
}
size_type size() const noexcept {
return taille();
}
class HorsBornes {};
value_type operator[](size_type n) const {
// if (!indice_legal(n)) throw HorsBornes{}; // si vous y tenez
return texte[n];
}
value_type& operator[](size_type n) {
// if (!indice_legal(n)) throw HorsBornes{}; // si vous y tenez
return texte[n];
}
};
#include <iostream>
#include <iterator>
#include <algorithm>
using namespace std;
ostream &operator<<(ostream &os, const chaine_pascal &c) {
copy(begin(c), end(c), ostream_iterator<chaine_pascal::value_type>{os});
return os;
}
int main() {
chaine_pascal c = "Allo!";
cout << c;
}
Conteneurs standards
La bibliothèque standard de C++
inclut une partie qui est une bibliothèque en soi, mais une bibliothèque de conteneurs et d'algorithmes d'une grande élégance et
d'une grande efficacité. Cette bibliothèque est ce que plusieurs nomment la STL.
On y trouve une gamme intéressante de conteneurs standard comme le vecteur
(tableau dynamique), la liste simplement chaînée, la liste doublement
chaînée, la pile, la file, le tableau associatif, la liste avec
priorités, l'arbre balancé, etc.
Tous les conteneurs standard offrent une liste d'opérations unifiée
sur laquelle on peut compter et qui permet de développer des algorithmes
efficaces pour l'ensemble des conteneurs pris de manière générique.
Parmi ces opérations, on trouve :
La fin de la séquence est, comme
dans le cas du tableau plus haut, le premier élément suivant
le dernier élément valide de la séquence.
- L'opération push_back() pour insérer un
élément à la fin du conteneur (à la fin de la séquence définie par les
itérateurs de ce conteneur)
- Le prédicat empty() pour savoir si le
conteneur est vide ou non
- L'opération front() pour obtenir une
référence sur le premier élément de la séquence
- L'opération begin() pour obtenir un
itérateur sur le début de la séquence, et
- L'opération end() pour obtenir un itérateur
sur la fin de la séquence
En général, depuis C++ 11,
par souci de généralité, on préférera écrire
begin(v) et end(v) plutôt que
v.begin() et v.end() pour un conteneur
v donné, du fait que cette écriture est plus générale
(elle s'applique même aux tableaux bruts).
Tout conteneur standard décrit, à l'interne, le concept d'itérateur
tel qu'il apparaît pour lui. Pour un vecteur, dont la représentation
interne est un tableau dynamique, un itérateur est essentiellement un
pointeur sur un élément, et l'opération
++ sur un itérateur y est l'opération arithmétique
primitive menant un pointeur vers l'élément suivant du tableau.
Pour une liste simplement chaînée, un itérateur est un objet
dont l'opérateur ++ fait passer l'itérateur
d'un noeud de la liste au noeud suivant.
Les itérateurs décrits par un conteneur donné se déclinent
en plusieurs saveurs, incluant les itérateurs unidirectionnels (qui définissent
++), bidirectionnels (qui ajoutent l'opérateur
-- à ceux que supportent les itérateurs unidirectionnels),
les itérateurs à accès direct (qui ajoutent les opérateurs
+=, -= et
[] à ceux supportés par les itérateurs bidirectionnels)
les itérateurs inversés (qui permettent de parcourir la séquence
en ordre inverse) et les itérateurs constants (à travers lesquels
il est impossible de modifier un élément d'une séquence).
Conteneur standard type – le vecteur
|
Le fait que la taille d'un tableau soit fixée
de sa création à sa destruction constitue un irritant pour bien
des applications, ce qui a mené à une prolifération des
tableaux dits dynamiques, donc de structures offrant à la fois la rapidité
d'accès à un élément d'un tableau et
la capacité de croître en fonction des besoins.
L'exemple à droite insère les entiers 1
à 10 dans un vecteur. L'opération
push_back() réalise l'insertion d'un élément à
la fin de la séquence que constitue un vecteur.
|
#include <vector>
int main() {
using std::vector;
vector<int> v;
for (int i = 0; i < 10; ++i)
v.push_back(i+1);
}
|
La mémoire à l'intérieur du vecteur est allouée
de manière dynamique. Le destructeur du vecteur assure la bonne libération
de l'espace attribué à l'entreposage des éléments.
Règle générale, les conteneurs standards peuvent manipuler
des éléments qui peuvent être copiés ou, en C++ 11,
déplacés.
| Le vecteur est,
avec raison, perçu comme le conteneur standard par défaut.
C'est lui qui, en moyenne, offre les meilleures performances pour
la majorité des applications. Cela dit, le choix d'un conteneur
ne doit pas être fait à l'aveuglette et nous essaierons
de faire des choix qui seront rigoureux et réfléchis lorsque
nous aurons besoin d'un conteneur.
Les algorithmes définis de manière à opérer sur
des itérateurs opèrent aussi rapidement sur un vecteur standard
que sur un tableau car, après tout, à l'interne, ces deux entités
sont essentiellement identiques. Les
vecteurs sont même plus rapides que les tableaux bruts pour qui sait
les utiliser adéquatement.
L'exemple à
droite offre une illustration de cette similitude, et montre du même
coup la beauté des algorithmes se voulant génériques:
ceux-ci peuvent être écrits une seule fois de manière
efficace et générale, puis appliqués à tout
conteneur sur lequel peut s'appliquer le concept d'itérateur. |
#include <vector>
#include <algorithm>
int main() {
using namespace std;
const int N = 100;
int tab[N];
vector<int> v;
for (int i = 0; i < N; ++i) {
tab[i] = i+1;
v.push_back(i+1);
}
inverser(begin(tab), end(tab));
inverser(begin(v), end(v));
}
|
Résultat : gain net de généricité, donc moins
de code à écrire et à mettre à jour, et aucune perte
de performance à l'exécution.
Principale force : vitesse d'accès à un
élément du conteneur.
Principale faiblesse : les opérations d'insertion
et de suppression ailleurs qu'à la fin de ce conteneur sont plus lentes
que les opérations équivalentes sur une liste.
Impact : de manière générale, les
opérations applicables à une séquence sans en changer la
taille tendent à être plus rapide sur un vecteur que sur d'autres
conteneurs. Ceci inclut les opérations de tri et, à un moindre
degré, la majorité des parcours de séquence.
Autres conteneurs standards capables de représenter
une séquence
Une file doublement chaînée, ou
std::deque, offre
de meilleures performances que
std::vector pour
ce qui est des opérations aux extrémités, est un peu plus
efficace que
std::vector pour les insertions et
les suppressions en un point arbitraire de la séquence, mais est moins
efficace pour accéder à un élément quelconque de
la séquence.
Une liste doublement chaînée, ou
std::list,
sera un peu plus efficace que
std::vector ou
std::deque lorsque les opérations d'insertion et de suppression
à réaliser sur la séquence seront nombreuses.
Conteneurs standards et performance – des comparatifs
Procédons
à quelques comparatifs sur l'emploi de conteneurs standard
et de conteneurs primitifs comme les tableaux.
Test 0.0 :
insérer des éléments à la fin d'une séquence.
#include <chrono>
#include <vector>
#include <iostream>
#include <list>
#include <deque>
using namespace std;
using namespace std::chrono;
template <class C>
auto inserer_elements(C &conteneur, int nelems) {
auto avant = system_clock::now();
for (int i = 0; i < nelems; ++i) conteneur.push_back(i+1);
return system_clock::now() - avant;
}
int main() {
const int NINSERTIONS = 5'000'000;
vector<int> v;
list<int> lst;
deque<int> d;
auto t_v = inserer_elements(v, NINSERTIONS);
auto t_lst = inserer_elements(lst, NINSERTIONS);
auto t_d = inserer_elements(d, NINSERTIONS);
cout << "Résultats pour " << NINSERTIONS << " insertions (ms):"
<< "\n\tvector: " << duration_cast<milliseconds>(t_v)
<< "\n\tlist: " << duration_cast<milliseconds>(t_lst)
<< "\n\tdeque: " << duration_cast<milliseconds>(t_d) << endl;
}
Question : lorsque le tout est compile en mode Release,
lequel de ces conteneurs offrira les meilleures performances au test proposé
ici?
Test 0.0b :
si, dans l'opération en gras dans la fonction de test ci-dessus, nous
remplaçons l'opération insérant à la fin...
template <class C>
auto inserer_elements(C &conteneur, int nelems) {
auto avant = system_clock::now();
for (int i = 0; i < nelems; ++i) conteneur.push_back(i+1);
return system_clock::now() - avant;
}
...par une opération insérant au début...
template <class C>
auto inserer_elements(C & conteneur, int nelems) {
auto avant = system_clock::now();
for (int i = 0; i < nelems; ++i) conteneur.insert(conteneur.begin(),i+1);
return system_clock::now() - avant;
}
...alors lequel des conteneurs examinés offrira la meilleure performance?
Prudence : insérer au début est, pour la plupart des conteneurs,
une opération un peu plus lente qu'insérer à la fin, alors
il est possible que vous souhaitiez réduire le nombre d'insertions réalisées
dans le test par un facteur de 100.
Test 0.1 :
trier les éléments d'une séquence. Contrairement aux tests
réalisant des insertions, qui nécessitent des conteneurs dont
la capacité d'entreposage peut croître au besoin, celui-ci peut
se faire autant sur un tableau que sur un conteneur plus dynamique, mais nécessite
des itérateurs ayant la propriété qu'on puisse évaluer
la distance entre deux instances d'itérateur (ce qui disqualifie les
listes dont les noeuds ne sont pas nécessairement disposés de
manière croissante ou décroissante en mémoire).
#include <ctime>
#include <algorithm>
#include <vector>
#include <iostream>
#include <deque>
#include <random>
#include <memory>
using namespace std;
using namespace std::chrono;
template <class It>
auto trier_elements(It debut, It fin) {
auto avant = system_clock::now();
sort(debut, fin);
return system_clock::now() - avant;
}
int main() {
const int NELEMS = 5'000'000;
unique_ptr<int[]>tab { new int[NELEMS] };
for (int i = 0; i < NELEMS; ++i)
tab[i] = i + 1;
random_device rd;
mt19937 prng{ rd() };
shuffle(&tab[0], &tab[NELEMS], prng);
// par souci d'intégrité, tous nos conteneurs contiendront la même
// séquence pour la réalisation du tri demandé
vector<int> v{&tab[0], &tab[NELEMS]};
deque<int> d{&tab[0], &tab[NELEMS]};
auto t_t = trier_elements(&tab[0], &tab[NELEMS]);
auto t_v = trier_elements(begin(v), end(v));
auto t_d = trier_elements(begin(d), end(d));
cout << "Résultats pour le tri de " << NELEMS << " éléments (ms):"
<< "\n\ttableau: " << duration_cast<milliseconds>(t_t)
<< "\n\tvector: " << duration_cast<milliseconds>(t_v)
<< "\n\tdeque: " << duration_cast<milliseconds>(t_d) << endl;
}
Question : lorsque le tout est compile en mode Release,
lequel de ces conteneurs offrira les meilleures performances au test proposé
ici? Utiliser un tableau pour une opération de tri est-il avantageux
si on compare les résultats à ceux obtenus pour le tri d'un vecteur?
Y a-t-il une différence significative entre le vecteur et les autres
conteneurs standard examinés?
Test 0.2 (exercice) :
construisez un tableau trié de grande taille contenant des valeurs générées
aléatoirement. Copiez ces valeurs dans divers conteneurs standard de
manière à ce que chacun ait les mêmes valeurs dans le même
ordre. Cherchez ensuite dans chaque conteneur une centaine de valeurs prises
aléatoirement à l'aide de l'algorithme standard
std::binary_search()
qui réalise une recherche dichotomique. Une fois que le tout aura
été compile en mode Release, lequel de ces conteneurs
offrira les meilleures performances au test proposé ici? Utiliser un
tableau pour une opération de tri est-il avantageux si on compare les
résultats à ceux obtenus pour le tri d'un vecteur? Y a-t-il une
différence significative entre le vecteur et les autres conteneurs standard
examinés?
Remarques sur la nature des tests réalisés
dans cette section
Nous avons pris soin, dans les tests de cette section, de
ne pas comparer (comme le veut l'adage) des pommes avec des
oranges.
Ainsi, dans Test 0.0,
nous souhaitions comparer la performance de divers conteneurs standard de capacité
dynamique lors d'opérations d'insertion en fin de séquence. Pour
y arriver, nous avons isolé l'opération en question pour que les
conditions soient précisément les mêmes pour tous les conteneurs
comparés, de sorte que seule la manière d'insérer, propre
à chaque conteneur, soit de nature à influer sur les résultats.
Notons toutefois que
dans des cas comme celui du tri, il aurait été possible
d'exploiter des stratégies plus performantes en fonction
du conteneur sollicité, par exemple avec la classe std::list pour laquelle la stratégie
standard de tri est inopérante.
Dans Test 0.0b,
nous souhaitions comparer la performance de divers conteneurs standard de capacité
dynamique lors d'opérations d'insertion en début de séquence.
La même prudence s'imposait, clairement.
Dans Test 0.1,
la qualité du tri pourrait être influencé par la disposition
originale des éléments dans le conteneur (selon la stratégie
de tri utilisée, cela peut influencer le nombre de permutations
à réaliser). Pour nos fins, il semblait approprié
d'appliquer la même stratégie de tri sur des conteneurs dont
le contenu était, à l'origine, précisément
le même (mêmes éléments, du même type,
dans le même ordre).
Opérer sur
des séquences
Rassembler des entités opérationnellement ou structurellement
semblables est chose commune en situation de développement informatique.
On réunit les noms dans un bottin pour les mettre en ordre et faciliter
les recherches de numéros de téléphone; on groupe les clients
d'une entreprise pour être en mesure de leur envoyer de la publicité;
on groupe les objets dessinables pour faciliter un affichage rapide
sur une surface; on groupe les entités mobiles pour pouvoir les déplacer
plus facilement; etc.
Il existe une maxime simple, qu'on pourrait probablement
sans gêne qualifier de loi conceptuelle, selon laquelle il est
plus simple d'opérer sur une entité que sur un groupe d'entités,
l'effort requis pour réaliser le travail sur un groupe impliquant
nécessairement celui requis pour opérer sur une seule entité
en plus de l'effort requis pour mettre au point la logique propre au
groupe (compteur, test de la condition de poursuite d'une répétitive,
portée des variables propres au traitement sur une entité, etc.).
Traditionnellement, la tendance opératoire était
de travailler sur les séquences tout entières plutôt que
sur des éléments pris isolément parce que cela semblait
(avec raison) plus rapide. Appeler une fonction pour traiter un élément
d'une séquence, et ce pour chaque élément, représentait
pour la plupart des programmes soumis à des contraintes strictes de
performance un coût prohibitif.
Heureusement, nous avons progressé, et nous sommes
maintenant en possession d'outils conceptuels permettant d'être
à la fois élégants et efficaces dans notre travail.
Il existe plusieurs manières d'opérer sur une séquence :
-
À l'aide d'opérations insérées à même le corps de la répétitive appelante
-
À l'aide d'opérations reposant sur des variables globales mais insérées
dans une fonction
-
À l'aide d'opérations reposant sur une
fonction paramétrée, et
-
À l'aide de foncteurs
Nous procéderons à des comparatifs simples
pour saisir l'impact de chacun de ces choix.
Test 1.0 :
comptabiliser des données sur les éléments d'une séquence,
en utilisant du code inséré à même la répétitive
appelante. Ce test peut se faire autant sur un tableau que sur un conteneur
plus dynamique. Remarquez que le code est répétitif et qu'il est
facile de commettre une erreur (comme par exemple oublier de réinitialiser
la somme à 0).
#include <vector>
#include <list>
#include <deque>
#include <iostream>
#include <random>
#include <memory>
#include <chrono>
#include <algorithm>
using namespace std;
using namespace std::chrono;
int main() {
const int NELEMS = 5'000'000;
unique_ptr<int[]> tab{ new int[NELEMS] };
random_device rd;
mt19937 prng{ rd() };
uniform_int_distribution<int> distrib{ 1, 10 };
for (int i = 0; i < NELEMS; ++i)
tab[i] = distrib(prng);
// par souci d'intégrité, tous nos conteneurs contiendront la même
// séquence pour la réalisation du tri demandé
vector<int> v{ &tab[0], &tab[NELEMS] };
list<int> lst{ &tab[0], &tab[NELEMS] };
deque<int> d{ &tab[0], &tab[NELEMS] };
long somme;
// Test sur le tableau (avec index)
long somme {};
auto avant = system_clock::now();
for (int i = 0; i < NELEMS; ++i)
somme += tab[i];
auto apres = system_clock::now();
auto t_t0 = apres-avant;
// Test sur le tableau (avec index)
somme = {};
auto avant = system_clock::now();
for (int *p = tab; p != tab+NELEMS; ++p) somme += *p;
apres = system_clock::now();
auto t_t1 = apres-avant;
// Test sur un std::vector
somme = {};
avant = system_clock::now();
for (auto it = begin(v); it != end(v); ++it) somme += *it;
apres = system_clock::now();
auto t_v = apres-avant;
// Test sur une std::list
somme = {};
avant = system_clock::now();
for (auto it = begin(lst); it != end(lst); ++it) somme += *it;
apres = system_clock::now();
auto t_lst = apres-avant;
// Test sur une std::deque
somme = {};
avant = system_clock::now();
for (auto it = begin(d); it != end(d); ++it) somme += *it;
apres = system_clock::now();
auto t_d = apres-avant;
cout << "Résultats pour la somme de " << NELEMS << " éléments (ms):"
<< "\n\ttableau (index): " << duration_cast<milliseconds>(t_t0)
<< "\n\ttableau (itérateur): " << duration_cast<milliseconds>(t_t1)
<< "\n\tvector: " << duration_cast<milliseconds>(t_v)
<< "\n\tlist: " << duration_cast<milliseconds>(t_lst)
<< "\n\tdeque: " << duration_cast<milliseconds>(t_d) << endl;
}
Question : laquelle des cinq stratégies permet
ici le parcours le plus rapide? Notez que si vous augmentez le nombre d'éléments
à examiner, ce genre de test peut devenir très coûteux en
mémoire, ce qui implique que vous voudrez peut-être réduire
la portée (peut-être en insérant des blocs anonymes) des
diverses variables impliquées.
Test 1.1 :
comptabiliser des données sur les éléments d'une séquence
en utilisant une variable globale comme variable d'accumulation. Ce test peut
se faire autant sur un tableau que sur un conteneur plus dynamique.
#include <vector>
#include <list>
#include <deque>
#include <iostream>
#include <chrono>
#include <algorithm>
#include <random>
#include <memory>
using namespace std;
using namespace std::chrono;
namespace {
long g_Somme = {};
}
template <class It>
auto somme_elements(It debut, It fin) {
g_Somme = {};
auto avant = system_clock::now();
for (; debut != fin; ++debut) g_Somme += *debut;
return system_clock::now() - avant;
}
int main() {
const int NELEMS = 5'000'000;
unique_ptr<int[]> tab{ new int[NELEMS] };
random_device rd;
mt19937 prng{ rd() };
uniform_int_distribution<int> distrib{ 1, 10 };
for (int i = 0; i < NELEMS; ++i)
tab[i] = distrib(prng);
// par souci d'intégrité, tous nos conteneurs contiendront la même
// séquence pour la réalisation du tri demandé
vector<int> v{ &tab[0], &tab[NELEMS] };
list<int> lst{ &tab[0], &tab[NELEMS] };
deque<int> d{ &tab[0], &tab[NELEMS] };
auto t_t = somme_elements(&tab[0], &tab[NELEMS]);
auto t_v = somme_elements(begin(v), end(v));
auto t_lst = somme_elements(begin(lst), end(lst));
auto t_d = somme_elements(begin(d), end(d));
cout << "Résultats pour la somme de " << NELEMS << " éléments (ms):"
<< "\n\ttableau: " << duration_cast<milliseconds>(t_t)
<< "\n\tvector: " << duration_cast<milliseconds>(t_v)
<< "\n\tlist: " << duration_cast<milliseconds>(t_lst)
<< "\n\tdeque: " << duration_cast<milliseconds>(t_d) << endl;
}
Question : lequel des quatre conteneurs permet ici le
parcours le plus rapide? Constatez-vous une perte de performance en comparaison
avec la version sans fonction?
Test 1.2 :
comptabiliser des données sur les éléments d'une séquence
en utilisant un paramètre par référence comme variable
d'accumulation. Ce test peut se faire autant sur un tableau que sur un conteneur
plus dynamique.
#include <vector>
#include <list>
#include <deque>
#include <iostream>
#include <chrono>
#include <algorithm>
#include <random>
#include <memory>
using namespace std;
using namespace std::chrono;
template <class It>
auto somme_elements(It debut, It fin, long &somme) {
somme = {};
auto avant = system_clock::now();
for (; debut != fin; ++debut) somme += *debut;
return system_clock::now() - avant;
}
int main() {
const int NELEMS = 5'000'000;
unique_ptr<int []> tab{ new int[NELEMS] };
random_device rd;
mt19937 prng{ rd() };
uniform_int_distribution<int> distrib{ 1, 10 };
for (int i = 0; i < NELEMS; ++i)
tab[i] = distrib(prng);
long somme;
// par souci d'intégrité, tous nos conteneurs contiendront la même
// séquence pour la réalisation du tri demandé
clock_t t_t = somme_elements(&tab[0], &tab[NELEMS], somme);
vector<int> v{ &tab[0], &tab[NELEMS] };
list<int> lst{ &tab[0], &tab[NELEMS] };
deque<int> d{ &tab[0], &tab[NELEMS] };
auto t_v = somme_elements(begin(v), end(v), somme);
auto t_lst = somme_elements(begin(lst), end(lst), somme);
auto t_d = somme_elements(begin(d), end(d), somme);
cout << "Résultats pour la somme de " << NELEMS << " éléments (ms):"
<< "\n\ttableau: " << duration_cast<milliseconds>(t_t)
<< "\n\tvector: " << duration_cast<milliseconds>(t_v)
<< "\n\tlist: " << duration_cast<milliseconds>(t_lst)
<< "\n\tdeque: " << duration_cast<milliseconds>(t_d) << endl;
}
Question : lequel des quatre conteneurs permet ici le
parcours le plus rapide? Constatez-vous une perte de performance en comparaison
avec la version sans fonction? Constatez-vous une perte de performance en comparaison
avec la version réalisant l'accumulation avec une variable globale?
Test 1.3 :
comptabiliser des données sur les éléments d'une séquence
en utilisant un paramètre par référence comme variable
d'accumulation et en ayant recours à un foncteur. Ce test peut se faire
autant sur un tableau que sur un conteneur plus dynamique.
#include <vector>
#include <list>
#include <deque>
#include <iostream>
#include <chrono>
#include <algorithm>
#include <random>
#include <memory>
using namespace std;
using namespace std::chrono;
class Sommation {
long &cumul;
public:
Sommation(long &dest) noexcept : cumul{dest} {
}
void operator()(int val) noexcept {
cumul += val;
}
};
template <class It>
auto somme_elements(It debut, It fin, long &somme) {
somme = {};
autpo avant = system_clock::now();
for_each(debut, fin, Sommation{somme});
return system_clock::now - avant;
}
int main() {
const int NELEMS = 5'000'000;
unique_ptr<int[]> tab{ new int[NELEMS] };
random_device rd;
mt19937 prng{ rd() };
uniform_int_distribution<int> distrib{ 1, 10 };
for (int i = 0; i < NELEMS; ++i)
tab[i] = distrib(prng);
long somme;
// par souci d'intégrité, tous nos conteneurs contiendront la même
// séquence pour la réalisation du tri demandé
auto t_t = somme_elements(&tab[0], &tab[NELEMS], somme);
vector<int> v{ &tab[0], &tab[NELEMS] };
list<int> lst{ &tab[0], &tab[NELEMS] };
deque<int> d{ &tab[0], &tab[NELEMS] };
auto t_v = somme_elements(begin(v), end(v), somme);
auto t_lst = somme_elements(begin(lst), end(lst), somme);
auto t_d = somme_elements(begin(d), end(d), somme);
cout << "Résultats pour la somme de " << NELEMS << " éléments (ms):"
<< "\n\ttableau: " << duration_cast<milliseconds>(t_t)
<< "\n\tvector: " << duration_cast<milliseconds>(t_v)
<< "\n\tlist: " << duration_cast<milliseconds>(t_lst)
<< "\n\tdeque: " << duration_cast<milliseconds>(t_d) << endl;
}
Question : lequel des quatre conteneurs permet ici le
parcours le plus rapide? Constatez-vous une perte de performance en comparaison
avec la version sans fonction? Constatez-vous une perte de performance en comparaison
avec la version réalisant l'accumulation avec une variable globale? Constatez-vous
une perte de performance en comparaison avec la version réalisant l'accumulation
avec un paramètre par référence et une boucle artisanale?
Algorithmes standards
La standardisation des opérations sur des séquences à
travers le concept d'itérateur a conduit à la production d'algorithmes
standard, plusieurs d'entre eux étant livrés dans le fichier d'en-tête <algorithm>.
Nous avons déjà rencontré std::sort(),
qui trie[2] une
séquence située entre deux itérateurs, de même que random_shuffle()
qui mélange les éléments d'une séquence avec
une série de permutations aléatoires et que for_each() qui
applique une opération à tous les éléments d'une
séquence:
| Ceci... |
...équivaut à ceci |
T tab[N] { /* ... */ };
for (auto p= begin(tab); p != end(tab); ++p)
op(*p);
|
T tab[N] { /* ... */ };
for_each(begin(tab), end(tab), op);
|
Le Test 1.3
a permis de montrer que for_each()
n'entraînait aucune perte de performance en comparaison avec une
boucle for normale si cette dernière était
écrite avec soin. Les avantages de for_each()
sur une boucle for sont multiples :
-
La standardisation de la représentation des extrémités
de la séquence permet d'éliminer presque en totalité
toute erreur de contrôle de répétitive (indice mal choisi,
vérification des bornes, manipulation incorrecte des pointeurs, etc.))
- Les risques d'une erreur technique menant à une répétitive
de qualité non optimale sont fortement réduits, l'algorithme for_each()
réalisant la meilleure forme répétitive possible pour la plateforme –
autrement dit, il est possible, dans le cas général, de faire aussi bien
manuellement, mais pas de faire mieux
-
La problématique d'appliquer une opération
à chaque élément d'une séquence étant
réglée de facto par l'algorithme, le programmeur
peut se concentrer sur la manière la plus efficace de réaliser
une opération précise sur un élément de la séquence,
quel qu'il soit. Cette réduction du domaine du problème
facilite la rédaction de code clair et efficace.
Il existe évidemment bien d'autres algorithmes
standard. Les connaître et les utiliser accroît la réutilisation
du code, réduit la quantité de tests à réaliser,
et offre automatiquement des garanties de performance, ce qui permet aux programmeurs
de concentrer leurs efforts ailleurs.
Test 2.0 :
compter le nombre d'entités inactives dans une séquence.
#include <chrono>
#include <random>
#include <algorithm>
#include <vector>
#include <iostream>
using namespace std;
using namespace std::chrono;
// Pour les fins de notre test, une entite aura une chance sur deux en moyenne d'être inactive
namespace {
random_device rd;
mt19937 prng{rd()};
uniform_int_distribution<int> distrib{ 0, 1 };
}
class Entite {
bool actif;
public:
Entite() : actif{distrib(prng) != 0 } {
}
bool est_inactive() const noexcept {
return !actif;
}
};
// Le compte manuel teste chaque Entite et incrémente le
// compteur d'entités inactives seulement dans le cas où
// celle examinée est inactive
template <class It>
auto compter_inactifs_manuel(It debut, It fin, int &n) {
n = {};
auto avant = system_clock::now();
for (; debut != fin; ++debut)
if (debut->est_inactive()) ++n;
return system_clock::now() - avant;
}
// Le compte standard utilise l'algorithme standard count_if()
template <class It>
auto compter_inactifs_std(It debut, It fin, int &n) {
auto avant = system_clock::now();
n = count_if(debut, fin, [](const Entite &e) { return e.est_inactive(); });
return system_clock::now() - avant;
}
int main() {
const int NELEMS = 50'000'000;
vector<Entite> v{ NELEMS };
int n;
auto t_man = compter_inactifs_manuel(begin(v), end(v), n);
cout << "Compatibilité manuelle, nb d'inactifs sur " << NELEMS << " éléments: "
<< n << ", temps requis (ms):" << duration_cast<milliseconds>(t_man) << endl;
auto t_std = compter_inactifs_std(begin(v), end(v), n);
cout << "Compatibilité standard, nb d'inactifs sur " << NELEMS << " éléments: "
<< n << ", temps requis (ms):" << duration_cast<milliseconds>(t_std) << endl;
}
Question : réalisez ce test plusieurs fois. Quelle
est la proportion de tests pour laquelle l'algorithme comptabilisant les entités
inactives manuellement offrira une meilleure performance que ne le fait l'algorithme
standard?
Test 2.1 :
trouver le premier expert dans une séquence où on trouve un expert
et une multitude de néophytes.
#include <chrono>
#include <random>
#include <algorithm>
#include <vector>
#include <iostream>
#include <vector>
using namespace std;
using namespace std::chrono;
// Pour les fins de notre test, une Entite par défaut sera considérée néophyte,
// jusqu'à ce qu'elle ait été promue à un autre rôle
namespace {
random_device rd;
mt19937 prng{rd()};
uniform_int_distribution<int> distrib{0, 1};
}
class Entite {
enum Grade { NEOPHYTE, APPRENTI, ADEPTE, EXPERT, MAITRE };
Grade grade_ { NEOPHYTE };
public:
Entite() = default;
Grade grade() const noexcept {
return grade_;
}
bool promotion() noexcept {
if (grade() == MAITRE)
return false;
grade_ = static_cast<Grade>(grade() + 1);
return true;
}
bool est_expert() const noexcept {
return grade() >= EXPERT;
}
};
// La recherche manuelle est légèrement inélégante mais a été écrite de manière
// à laisser le moins de place possible à la critique. Dès qu'un expert a été
// trouvé, cette fonction calcule le temps requis pour la recherche qui vient de
// se terminer et retourne un itérateur sur l'élément trouvé
template <class It>
It trouver_expert_manuel(It debut, It fin, system_clock::duration &temps) {
auto avant = system_clock::now();
for (; debut != fin; ++debut)
if (debut->est_expert()) {
temps = system_clock::now - avant;
return debut;
}
temps = system_clock::now - avant;
return fin;
}
// La recherche standard utilise l'algorithme find_if()
#include <algorithm>
template <class It>
It trouver_expert_std (It debut, It fin, clock_t &temps) {
auto avant = system_clock::now();
It it = find_if(debut, fin, [](const Entite &e) { return e.est_expert(); });
temps = system_clock::now - avant;
return it;
}
int main() {
const int NELEMS = 5'000'000;
vector<Entite> v{NELEMS};
// Promotion de la première entité au rang d'expert
{
auto &e = v.front();
while (!e.est_expert())
e.promotion();
}
// On brasse la séquence... où est rendu l'expert?
shuffle(begin(v), end(v), prng);
{
system_clock::duration t_man;
auto itt = trouver_expert_manuel(begin(v), end(v), t_man);
cout << "Recherche manuelle sur " << NELEMS
<< " éléments: position" << distance(begin(v), itt)
<< ", temps requis (ms): " << duration_cast<milliseconds>(t_man) << endl;
}
{
system_clock::duration t_std;
auto itt = trouver_expert_std(begin(v), end(v), t_std);
cout << "Recherche standard sur " << NELEMS
<< " éléments: position" << distance(begin(v), itt)
<< ", temps requis (ms): " << duration_cast<milliseconds>(t_std) << endl;
}
}
Question : réalisez ce test plusieurs fois. Quelle
est la proportion de tests pour laquelle l'algorithme réalisant la recherche
manuelle d'entités expertes offrira une meilleure performance que ne
le fait l'algorithme standard?
Test 2.2 :
trouver "Fred" dans une séquence
où on trouve un "Fred" et une multitude
de "Joe Blo". Ce test reprend Test
2.1 avec de légères
modifications de manière à utiliser std::find(),
qui repose sur l'opérateur == des objets
insérés dans la séquence, plutôt que std::find_if() qui repose sur un prédicat externe.
#include <chrono>
#include <random>
#include <algorithm>
#include <vector>
#include <iostream>
#include <vector>
#include <string>
using namespace std;
using namespace std::chrono;
// Nous ajoutons un nom à toute entité et les strates opérationnelles qui
// accompagnent ajout. L'opérateur == sur une Entite et une std::string
// retournera true si la chaîne standard correspond au nom de l'entité
class Entite {
enum Grade { NEOPHYTE, APPRENTI, ADEPTE, EXPERT, MAITRE };
Grade grade_ { NEOPHYTE };
string nom_ { "Joe Blo"s };
public:
Entite() = default;
Entite(const string &nom) : nom_{ nom } {
}
Grade grade() const noexcept {
return grade_;
}
string nom() const {
return nom_;
}
void renommer(const string &nom) {
nom_ = nom;
}
bool promotion() {
if (grade() == MAITRE)
return false;
grade_ = static_cast<Grade>(grade() + 1);
return true;
}
bool est_expert() const noexcept {
return grade() >= EXPERT;
}
bool operator==(const Entite &e) const {
return grade() == e.grade() && nom() == e.nom();
}
bool operator==(const string &s) const {
return nom() == s;
}
};
// Les recherches ont été légèrement adaptées pour tenir compte
// de la recherche par nom plutôt que par grade
template <class It>
It trouver_entite_manuel(It debut, It fin, const string &s, system_clock::duration &temps) {
auto avant = system_clock::now();
for (; debut != fin; ++debut)
if (*debut == s) {
temps = system_clock::now() - avant;
return debut;
}
temps = system_clock::now() - avant;
return fin;
}
// La recherche standard avec find() se base sur l'opérateur == de Entite
// et ne nécessite donc pas de prédicat externe pour réaliser sa tâche
#include <algorithm>
template <class It>
It trouver_entite_std(It debut, It fin, const string &s, system_clock::duration &temps) {
auto avant = system_clock::now();
It it = find(debut, fin, s);
temps = system_clock::now() - avant;
return it;
}
int main() {
const int NELEMS = 5'000'000;
vector<Entite> v{NELEMS};
// L'une des entités se nomme "Fred"
v.front().renommer("Fred");
// On brasse la séquence... où est rendu Fred?
shuffle(begin(v), end(v), prng);
{
system_clock::duration t_man;
auto itt = trouver_entite_manuel(begin(v), end(v), "Fred", t_man);
cout << "Recherche manuelle sur " << NELEMS
<< " éléments: position" << distance(begin(v), itt)
<< ", temps requis (ms):" << duration_cast<milliseconds>(t_man) << endl;
}
{
system_clock::duration t_std;
auto it = trouver_entite_std(begin(v), end(v), "Fred", t_std);
cout << "Recherche standard sur " << NELEMS
<< " éléments: position" << distance(begin(v), it)
<< ", temps requis (ms):" << duration_cast<milliseconds>(t_std) << endl;
}
}
Question : réalisez ce test plusieurs fois. Quelle
est la proportion de tests pour laquelle l'algorithme réalisant la recherche
manuelle d'une entité offrira une meilleure performance que ne le fait
l'algorithme standard?
Remarquez que tous les tests manuels demandent une forme d'artisanat :
chacun est adapté de manière locale, pour tenir compte des contraintes
propres au test en cours de réalisation. En retour, les algorithmes standards
ont une forme homogène et leur adaptation ne demande d'un test à
l'autre, que peu ou pas de modifications.
Points sur lesquels il convient de réfléchir
Nous devons tirer un certain nombre de leçons de ces tests, en prenant
bien soin de prendre ces leçons comme des recommandations, pas comme
un dogme – rien ne remplace la pensée critique et les mesures concrètes!
Mode d'opération
Dans la mesure du possible, il est préférable
de manipuler les séquences logées dans un conteneur conteneurs
à travers des itérateurs plutôt qu'à travers
des mécanismes moins génériques, du fait que cela permet
la conception d'algorithmes qui sont indépendants du substrat
organisationnel, et ainsi de réutiliser plus et mieux le code produit.
Notons qu'utiliser un indice dans un tableau demande
au compilateur de transformer la forme indicée en une forme proche
de celle d'un itérateur en réalisant une opération
arithmétique sur des pointeurs. Il n'y a donc aucunée perte de
généralité ou de performance à opérer sur
une séquence comme le tableau ou le vecteur à travers la métaphore
d'un itérateur.
Choix du conteneur
Les métriques simples faites ci-dessus sont des indicateurs
que les conteneurs standard, utilisés de manière appropriée
et choisis avec soin, permettent de maintenir (souvent d'augmenter) la
performance du code à l'exécution.
L'emploi de conteneurs standards a aussi un impact important sur la qualité
du code produit, et ce selon plusieurs points de vue :
-
Utiliser les conteneurs assure une standardisation du code produit
-
La standardisation du code permet la production d'algorithmes génériques
-
La généricité et la standardisation entraînent un accroissement important
du potentiel de réutilisation du code
-
La standardisation du code permet d'adoucir la courbe d'apprentissage que
rencontrent les gens qui y font face
-
Les conteneurs standard sont livrés avec des garanties de complexité
algorithmique et une documentation très claire
-
Les conteneurs standard ont été testés de manière exhaustive et peuvent
être utilisés avec confiance
À algorithme égal, un vecteur standard offre des performances
équivalentes (en fait, souvent
meilleures) à celles d'un tableau. Ceci brise en partie le mythe
selon lequel la
POO entraîne du code plus
lourd[3] et plus
lent que ne le fait la programmation procédurale.
Sachant que le vecteur offre à plusieurs égards
un meilleur niveau de sécurité qu'un tableau (capacité
de croître au besoin, destructeurs assurant la bonne libération
des ressources, taille disponible sur demande, bonne gestion du concept de
conteneur vide, etc.), il est souvent de bonne guerre de privilégier
l'usage d'un vecteur standard à celui d'un tableau.
Certaines circonstances peuvent rendre moins approprié
l'emploi d'un vecteur: les tableaux à deux dimensions ou
plus peuvent s'écrire sous forme de vecteur de vecteur (de vecteur...),
mais il est possible que la notation devienne rébarbative pour certains.
De même, les situations à forte teneur d'insertion et de
suppression ailleurs qu'à la fin d'un conteneur tiennent,
de par leur nature même, le vecteur en situation désavantageuse.
Le vecteur est donc un bon conteneur par défaut, mais
sans suffire à lui seul pour couvrir toutes les situations possibles
et envisageables. Une analyse critique du contexte d'utilisation demeure
nécessaire si l'objectif est de pondre un système informatique
efficace.
Périodes de turbulence organisationnelle
Selon les opérations à réaliser, il se peut que le conteneur
choisi pour la plupart des opérations ne soit, temporairement, plus l'option
idéale. Nous nommerons période de turbulence organisationnelle ces périodes dans la vie d'un programme où sont
comportement change drastiquement.
Une période de turbulence organisationnelle typique
est le passage d'une période où les opérations se
font massivement sur une séquence d'éléments à
faible variation (bouger régulièrement les personnages d'une
armée ou les vaisseaux d'une flottille; superviser l'équipement
dans une centrale nucléaire; projeter des objets graphiques sur une
surface bidimensionnelle; etc.) à une période où
se produisent de multiples insertions ou de multiples suppressions sur la
séquence (par exemple lors du chargement d'une grande quantité
de nouveaux éléments à partir d'une base de données).
Un trait marquant des périodes de turbulence organisationnelle
est que le conteneur usuel peut devenir un moins bon choix pendant la turbulence.
L'exemple typique est le vecteur, qui offre des performances plus qu'appréciables
dans la majorité des cas, mais dont les performances sont déplorables
dans certaines situations pathologiques – voir à cet effet Test 0.0b, plus haut.
Dans ce cas, plusieurs options sont possibles :
-
Si la période de turbulence est courte, il est possible qu'on décide de
conserver le conteneur par défaut et d'encaisser la dégradation temporaire
de performance
-
Si la période de turbulence risque de se prolonger, il est possible qu'on
privilégie de changer temporairement de conteneur, donc copier le contenu
du conteneur habituel dans un conteneur ayant une forme plus appropriée
aux besoins de la période de turbulence, de laisser passer la turbulence,
puis de recopier le contenu du conteneur temporaire dans le conteneur
habituel avant de poursuivre les opérations de manière plus normale
-
Si la situation s'y prête, on peut aussi envisager
de travailler temporairement à deux conteneurs, soit le conteneur usuel
pour les opérations normales et un conteneur auxiliaire pour la situation
turbulente, puis fusionner les deux au moment approprié. Ceci peut
être intéressant dans un jeu vidéo ou dans une situation
de type temps réel, où la fluidité et les stabilité
du système priment et où la turbulence provient de l'injection
dans le système de nouveaux éléments : le système
pourrait opérer en itérant à travers un vecteur pendant
qu'un thread auauxiliaire charge dans une liste des éléments
destinés à y être introduits, puis une fusion des deux conteneurs pourrait
être réalisée (en temps linéaire sur la somme de la taille des conteneurs,
dans bien des cas) de manière à réduire fortement l'impact de la
turbulence sur l'état global du système
Détection statique ou dynamique de turbulence
Il existe deux grandes catégories de détection de turbulence,
que nous qualifierons de détection statique et
de détection dynamique.
La détection statique de turbulence est la
plus fréquente. Tel que le veut l'usage, le terme statique signifie
ici connu au moment de la compilation.
On inclut dans cette catégorie toute situation prévisible:
l'initialisation d'un programme, par exemple, ou le chargement en
mémoire du contenu d'une zone susceptible d'être approchée
dans un jeu vidéo.
La détection dynamique de turbulence est plus délicate
et plus difficile à bien réaliser. Conséquemment, elle
est moins fréquente. On pense ici à un objet dans lequel on trouve
un conteneur (par exemple un moteur d'affichage contenant un vecteur de pointeurs
sur des objets dessinables et qui itère régulièrement sur
cette séquence pour tenir à jour l'affichage à l'écran).
Pour réaliser une détection dynamique de turbulence,
il faut avoir accès à une forme de modèle statistique
(si simple soit-il) de comportement normal et anormal. Un objet doit noter
les opérations réalisées sur lui et constater, éventuellement,
que le patron d'utilisation qu'on fait de lui a changé (par
exemple si le nombre d'insertions successives qui y ont été
réalisées ailleurs qu'à la fin vient de franchir
un certain seuil).
La turbulence est notée lorsque le comportement analysé
en continu par l'objet donne des signes d'anormalité. À
ce moment, l'objet tranche et change de conteneur jusqu'à
ce que les signes d'anormalité se soient atténués.
Il y a, visiblement, des risques importants à l'application
d'une stratégie dynamique de détection des turbulences.
On peut penser à une situation où les signes de normalité
et d'anormalité sont mal définis ou dans le cas où
les critères appliqués ne se prêtent pas au contexte dans
lequel l'objet est véritablement utilisé.
Une détection dynamique mal réalisée peut entraîner
de multiples copies de conteneur à conteneur, donc une dégradation
de performance semblable à celle qu'on rencontre en programmation système
lorsque des Page Faults ou des Cache Misses deviennent trop
fréquents – cette ressemblance n'est d'ailleurs pas fortuite puisque
l'analytique permettant de prévoir le contenu d'une antémémoire
ressemble beaucoup à celle propre à la détection de comportements
normaux ou anormaux autour de l'emploi d'un conteneur.
Notons que la plupart des systèmes ne prendront pas
la peine de réaliser une détection de turbulence, et que dans
les systèmes qui procèdent effectivement à une détection
de turbulence, le choix de la grande majorité sera de réaliser
une détection statique. C'est là le choix pragmatique.
Réaliser une détection dynamique de turbulence
La détection dynamique repose sur la saisie dynamique de données
quant à l'utilisation faite d'un conteneur – une encapsulation
stricte du conteneur dans un objet est une quasi nécessité pour
mener à bien une telle entreprise.
L'objet encapsulant le conteneur doit noter le nombre d'opérations de
chaque type et, dans la plupart des cas, le moment de ces opérations.
Par exemple, chaque parcours d'une séquence doit être noté,
de même que chaque insertion/ chaque extraction à la fin, au début
et ailleurs (trois métriques distinctes).
Chaque saisie de donnée doit être suivie d'un
appel à une méthode analytique à l'action très
rapide, capable de décider si le patron courant d'utilisation
est normal ou anormal et de provoquer sur-le-champ un changement de conteneur.
Une stratégie de ce genre implique un coût en
performance (saisie de données et analyse immédiate du profil
d'utilisation lors de chaque opération type sur le conteneur)
et en espace (pour entreposer les données saisies en cours de route).
Il faut donc analyser avec soin la situation avant de procéder à
la mise en place d'une telle mécanique. Historiquement, la plupart
des systèmes prévisionnels ont été des échecs:
ces systèmes sont difficiles à mettre en place et l'analyse
dynamique de turbulence est une chose difficile à faire, peu importe
la discipline.
Insertion d'intelligence analytique et approche client/
serveur
Dans les systèmes répartis, particulièrement ceux construits
selon une approche client/
serveur (CS), la détection dynamique
est une option plus raisonnable que dans les systèmes à fort couplage
comme le sont les applications monolithiques
OO ou
procédurales.
|
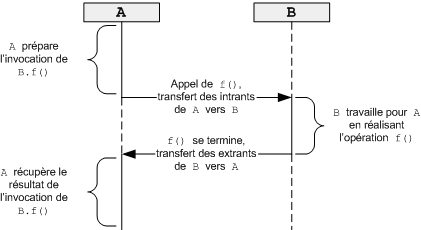
En effet, un appel
d'une méthode f() d'un objet B par
un objet A[4] est
un mécanisme immédiat qui cache l'image
plus traditionnelle selon laquelle, conceptuellement, A passe
le message f() à B.
Si B désire examiner à
un niveau méta son profil d'utilisation, il doit comptabiliser
les invocations de f() à
même f(), n'ayant pas lui-même de distance quant
à l'invocation de ses méthodes.
Le modèle
OO tel qu'implanté et proposé par la plupart des
langages
OO à vocation pragmatique occulte la mécanique
de passage de message en la représentant sous la forme plus immédiate
d'un appel de méthode. Cela permet entre autres au modèle
OO d'être assez efficace pour la construction d'applications
commerciales, avec le succès qu'on connaît.
|
 |
Cela dit, le modèle CS introduit une distance,
physique ou simplement conceptuelle, entre les homologues de la relation appelant/
appelé. L'échange d'information et de paires requête/ réponse
entre les homologues d'une relation CS est un formalisme
à part entière, sur lequel il est possible d'avoir une emprise
plus concrète que celle qu'on a habituellement sur la mécanique
d'invocation de méthodes.
|
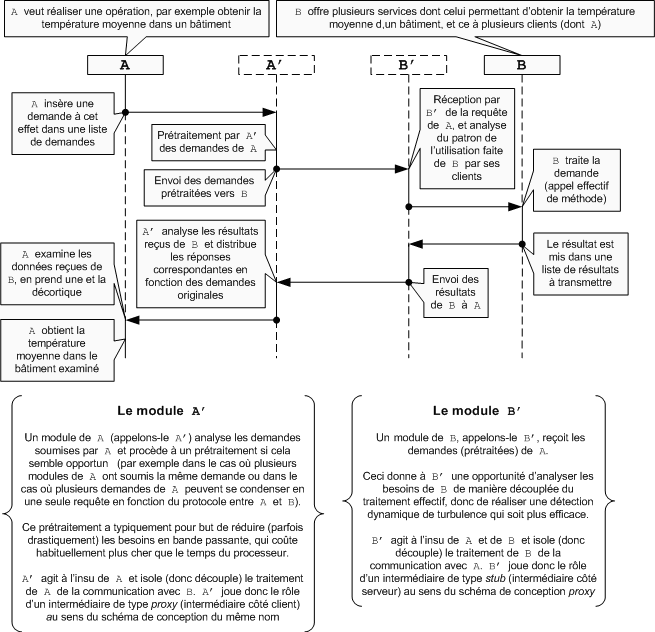
Ce formalisme sépare effectivement les désirs
du demandeur (l'appelant) de la requête soumise au serveur (l'appelé),
de même que la requête soumise au serveur de la méthode
invoquée en fin de compte. Cette distance réduit de beaucoup
la performance individuelle d'une requête prise individuellement,
mais tend à augmenter la performance d'ensemble du système.
En effet, la distance entre les homologues se prête à l'insertion
d'un découplage entre le traitement et la communication, découplage
pouvant être partiellement illustré par le schéma de conception
proxy.
Le demandeur insère ses demandes dans une liste, et un intermédiaire
côté demandeur réalise un prétraitement sur la liste
de demandes dans le but d'optimiser le volet communication et de réduire
la demande en bande passante.
Du côté serveur,
les requêtes reçues sont insérées dans une liste
et un prétraitement peut être réalisé sur les éléments
de cette liste afin, entre autres choses, d'en réaliser une analyse
et de détecter dynamiquement les périodes de turbulence structurelle,
et ce sans intrusion de la mécanique de détection des turbulences
dans le cours normal du traitement des demandes.
Ce caractère non intrusif d'une préoccupation
transverse (analyser les demandes soumises à un objet) est une caractéristique
qu'on retrouve aussi dans la programmation orientée aspect (POA), et qui suggère que les analyses dynamiques
de perturbation organisationnelle pourraient aussi être réalisées
de manière raisonnablement efficace à l'aide de telles
techniques.
|
 |
Coût d'une fonction
Un réflexe de programmation système est de
chercher à réduire le nombre d'invocations de sous-programmes
dans un système informatique, dans l'optique où chaque
appel entraîne un coût caché: conserver les registres sur
la pile, passer les paramètres, réaliser un saut inconditionnel
au lieu du sous-programme appelé, récupérer les paramètres,
etc.
Il y a un deuxième tranchant à la lame du inlining :
plus les sous-programmes grossissent et taille et en complexité et
moins un moteur d'optimisation sera en mesure de bien y travailler. Un abus
d'inlining ou l'application trop systématique de cette technique
sur des sous-programmes trop volumineux peut réduire la performance
d'ensemble du système plutôt que l'accroître.
Évidemment, le
inlining ne peut être appliqué à un sous-programme
récursif ou à une série de sous-programmes entraînant
une récursivité cyclique.
Dans cet ordre d'idées, on retrouve dans bien
des langages l'idée de inlining, ou de remplacement[5]
du code propre à l'appel d'un sous-programme par le code
du sous-programme appelé. Dans la mesure où le code appelé
est de petite taille, cette technique permet d'allier l'élégance
d'un code modulaire et la rapidité d'un code évitant
sélectivement les invocations de petits sous-programmes.
La qualité de l'application de cette stratégie
dépendra fortement de la qualité du moteur d'optimisation
de chaque compilateur.
En C++,
théoriquement, l'application du inlining devrait être
automatique pour toute méthode dont la définition et la déclaration
sont faites d'un seul trait (celles dont la définition se trouve à
même la déclaration de la classe) de même que pour les templates,
ceci parce que le compilateur est alors pleinement responsable de la mise en
application de la technique et a en mains tous les outils nécessaires
pour y parvenir.
En langage C
et C++,
le mot clé inline appliqué à
un sous-programme devrait aussi permettre d'indiquer au compilateur et à
l'éditeur de liens le souhait de faire remplacer les appels à
ce sous-programme par sa définition. Ce mot clé exige parfois
une collaboration entre l'éditeur de liens et le compilateur, ce qui
peut rendre sa mise en application plus laborieuse.
SaSachant tout cela, voici quelques remarques :
- Avec un compilateur convenable, il est aujourd'hui possible d'utiliser
des fonctions de petite taille pour représenter des séquences
d'opérations claires et bien définies sans que cela n'entraîne
une dégradation de la performance. Exprimé autrement :
il n'y a plus de raison réelle pour écrire de gros sous-programmes
dont le découpage laisserait à désirer[6].
La vitesse relative des systèmes contenant de grosses fonctions en
comparaison avec les systèmes contenant beaucoup de petites fonctions
d'une ou deux lignes est, aujourd'hui, un mythe;
- Les templates offrent aujourd'hui
le même niveau de « performance » (souvent mieux!) que les
macros, du fait
que le compilateur et son moteur d'optimisation peuvent y réaliser
les optimisations locales possibles sur les sous-programmes de petite taille,
que les types impliqués sont validés correctement, que les effets
de bord propres aux macros sont évités et ainsi de suite. La
vitesse relative des macros en comparaisons avec les fonctions est dont aussi,
aujourd'hui, un mythe. Considérant que les templates
offrent autant de généricité que les
macros tout
en améliorant radicalement la qualité et la robustesse du code,
on ne devrait aujourd'hui presque jamais avoir recours à une
macro
là où un template pourrait être
utilisé
- Lorsqu'au moins l'un des paramètres est fixé au préalable,
comme lorsque tous les éléments d'une séquence doivent
être projetés sur le même canevas ou sur le même
flux de sortie, alors il devient pertinent d'utiliser un foncteur plutôt
qu'une fonction, ce qui permet de combiner algorithme standard, approche
OO et d'obtenir à la fois souplesse, performance, réutilisation du
code et standardisation formelle
- Quand un algorithme comme
std::count_if() se
base sur un prédicat pour réaliser son travail et quand le prédicat
souhaité par le programmeur est une opération relationnelle
ou logique, il existe des prédicats standards pour réaliser le
travail et il est de bon aloi d'y avoir recours. Notez que les prédicats
tendent à être des fonctions, pas des foncteurs, et qu'il est
de rigueur d'utiliser std::binder1st() ou
std::binder2nd() pour lier l'un des deux paramètres à
la manière d'un foncteur typique
À titre d'exemple, l'extrait de code suivant compte le nombre d'éléments
de v, une séquence d'entiers arbitrairement
longue, qui sont négatifs.
#include <vector>#include <algorithm>
#include <iostream>
#include <functional>
int main() {
using namespace std;
vector<int> v;
for (int val; cin >> val; v.push_back(val))
;
cout << count_if(begin(v), end(v), binder2nd<less<int>>(less<int>{}, 0));
}
Les lieurs tels que binder2nd sont désuets depuis
C++ 11, étant d'abord remplacés par std::bind qui est plus
flexible et plus expressif :
#include <vector>
#include <algorithm>
#include <iostream>
#include <functional>
int main() {
using namespace std;
using namespace std::placeholders;
vector<int> v;
for (int val; cin >> val; v.push_back(val))
;
cout << count_if(begin(v), end(v), bind(less<int>{}, _1, 0));
}
Notez qu'avec C++ 11,
on aura surtout tendance à remplacer le code un peu lourd qui passe par un
foncteur
explicitement nommé par une simple expression
λ :
#include <vector>
#include <algorithm>
#include <iostream>
int main() {
using namespace std;
vector<int> v;
for (int val; cin >> val; v.push_back(val))
;
cout << count_if(begin(v), end(v), [](int n) {
return n < 0;
});
}
Avec
C++ 17, binder1st
et binder2nd seront dépréciés. S'il y a un outil avec lequel vous auriez avantage à devenir familières et familiers, c'est bien les expressions
λ.
Classes imbriquées
et optimisation des copies
Le Test 1.3
utilisait un foncteur dont l'attribut était une référence
à un entier long défini ailleurs, ce qui faisait de lui un outil
capable de réaliser une sommation à partir d'une variable externe.
Plusieurs algorithmes standard utilisent des opérations applicables à
un élément arbitraire d'une séquence (le cas archétypique
étant for_each()) mais sont rédigés
de manière à ce que l'opération soit passée par
valeur, ce qui devient vite un irritant lorsque l'opération est un foncteur.
Reprenons l'exemple de somme d'une séquence d'entiers, plus haut. Plutôt
que de réaliser la sommation comme nous l'avions fait :
template <class It>
auto somme_elements(It debut, It fin, long &somme) {
somme = {};
auto avant = system_clock::now();
for_each(debut, fin, Sommation{somme});
return system_clock::now() - avant;
}
Il aurait été plus élégant de procéder comme
suit :
template <class It>
auto somme_elements(It debut, It fin, long &somme) {
auto avant = system_clock::now();
Sommation s;
for_each(debut, fin, s);
somme = s.valeur();
return system_clock::now() - avant;
}
...de manière à ce que le foncteur encapsule à la fois l'opération
d'accumulation et la valeur cumulée. Cependant, le constructeur de copie
généré automatiquement par le compilateur réalise
une copie bit à bit des attributs de l'objet copié, ce qui rend
impraticable l'option suggérée ci-dessus (présumant que
le constructeur par défaut d'une Sommation initialise
l'attribut d'accumulation à 0, le fait que
for_each() reçoive l'opération par copie ferait en sorte
que s.valeur() retourne aussi
0, et ce peu importe la sommation réalisée par
for_each() et le foncteur s.
Une solution est de réécrire le foncteur
Sommation de manière à ce que copier une instance de Sommation fasse en sorte de partager la représentation de la Sommation originale avec celle de la copie, pour que le résultat
de la copie soit aussi celui de l'original. Idéalement, la représentation
interne de la somme sera dissociée de l'objet Sommation
et aura le profil d'un objet partageable.
Le code suit.
#include <memory>
template <class T>
class Sommation {
std::shared_ptr<T> p;
public:
Sommation() : p{ make_shared<T>(T{}) } {
}
template <class U>
void operator()(const U &val) {
*p += val;
}
T valeur() const {
return *p;
}
};
// La sommation se fait sur des int, le résultat sera un long
template <class It>
auto somme_elements(It debut, It fin, long &somme) {
somme = {};
auto avant = system_clock::now();
Sommation<long> s;
for_each(debut, fin, s);
somme = s.valeur();
return system_clock::now() - avant;
}
Cela dit, l'idiome privilégié dans STL
est le passage de paramètres par valeur, et on y privilégie
nettement la copie d'objets. Ainsi, un algorithme comme
for_each() aura essentiellement la signature suivante :
template <class It, class Op>
Op for_each(It debut, It fin, Op oper) {
for(; debut != fin; ++debut)
oper(*debut);
return oper;
}
Remarquez que l'opération y est copiée, puis utilisée
à l'interne de manière successive sur chaque élément
de la séquence pour enfin être
retournée, encore une fois par copie. Cela signifie que la manière
canonique d'exprimer (avec un
for_each(), car il
existe des algorithmes vraiment écrits spécifiquement pour réaliser
un cumul!) une sommation d'éléments serait plutôt :
class Somme {
long cumul{};
public:
Somme() = default;
constexpr Somme(long init) : cumul{ init } {
}
void operator()(int n) {
cumul += n;
}
long valeur() const {
return cumul;
}
};
template <class It>
auto somme_elements(It debut, It fin, long &somme) {
auto avant = system_clock::now();
somme = for_each(debut, fin, Somme{}).valeur();
return system_clock::now() - avant;
}
... ce qui est à la fois plus rapide, plus simple et plus élégant.
Évidemment, en choisissant le bon algorithme (accumulate(),
de la bibliothèque
<numeric>, dans
ce cas-ci), on se rapproche de l'optimalité :
template <class It>
auto somme_elements(It debut, It fin, long &somme) {
auto avant = system_clock::now();
somme = std::accumulate(debut, fin, long{});
return system_clock::now() - avant;
}
Ici, le cumul se fait par sommation, mais il est possible d'exprimer des produits,
des saisies de valeur maximale et autres résultats du genre en suppléant
en paramètre supplémentaire une fonction de cumul choisie en fonction
des besoins du code client.
Survol des principaux conteneurs standards
Ce qui suit n'est qu'un bref survol des conteneurs standards de
C++,
du moins en date de
C++ 14.
Les liens qui les accompagnent vous mènent vers l'aide en ligne officielle, qui
va beaucoup plus en détail dans chaque cas.
Conteneurs séquentiels
Ces conteneurs sont ceux que l'on privilégie lorsque l'un des objectifs est
d'opérer sur tous les éléments, un à la suite de l'autre.
| Conteneur |
Rôle |
Catégorie d'itérateurs |
Remarques |
|
vector<T>
|
Tableau dynamique de T. |
Random Access |
C'est le conteneur par défaut. Dans le doute, c'est probablement le
meilleur choix pour la majorité des applications... Et si vous pensez avoir
un cas pour lequel vector serait inadéquat,
faites quelques tests pour le vérifier empiriquement. Vous risquez d'avoir
toute une surprise... |
|
array<T,N>
|
Tableau de N éléments du type
T. Sert surtout à remplacer les tableaux bruts. |
Random Access |
Utile surtout si N est relativement petit
et s'il s'agit d'une valeur connue à la compilation. Ne supporte pas la
sémantique de mouvement. Peut être plus rapide
que vector<T> dans des cas ciblés |
|
deque<T>
|
Structure hybride facilitant les opérations aux extrémités |
Random Access |
Offre des caractéristiques de « performance » correctes mais
typiquement inférieures à celles de vector<T>.
Sert surtout à titre de substrat pour d'autres abstractions (voir
Adaptateurs de conteneurs, plus bas) |
|
list<T>
|
Liste doublement chaînée de T |
Bidirectional |
Surtout utile si (a) sizeof(T) est très
grand, (b) les insertions et suppressions d'éléments peuvent se faire un peu
partout dans le conteneur, et (c) s'il importe que les itérateurs sur
d'autres éléments que ceux insérés ou supprimés ne soient pas invalidés par
une insertion ou une suppression. |
|
forward_list<T>
|
Liste simplement chaînée de type T
|
Forward Only |
Se veut un exercice de minimalisme, en occupant très peu de mémoire |
Conteneurs associatifs
Ces conteneurs sont pensés pour garder leurs éléments dans un certain ordre
et pour faciliter l'insertion d'éléments de même que la recherche d'éléments.
Ils sont avantageux pour de grandes quantités d'éléments, mais avant d'écrire
beaucoup de code avec l'un d'eux, assurez-vous qu'un simple
vector<T> (ou vector<pair<K,V>>, selon le
cas) ne serait pas plus rapide.
| Conteneur |
Rôle |
Catégorie d'itérateurs |
Remarques |
|
set<T>
|
Ce conteneur permet d'entreposer des valeurs de telle manière que
chaque élément soit unique, et de telle sorte qu'ils soient toujours classés
en ordre selon un prédicat d'ordonnancement paramétrique |
Bidirectional |
Par défaut, l'ordonnancement se basera sur
less<T> |
|
map<K,V>
|
Ce conteneur permet d'entreposer des paires K, V (au sens de clé, valeur) de telle manière qu'il n'y ait qu'un seul V
pour chaque K, et de telle sorte que les clés
soient toujours classés en ordre selon un prédicat d'ordonnancement
paramétrique
|
Bidirectional |
Par défaut, l'ordonnancement se basera sur
less<K> |
|
multiset<T>
|
Comme set<T>,
mais admet plusieurs occurrences d'une même valeur |
Bidirectional |
|
|
multimap<K,V>
|
Comme
map<K,V>,
mais admet plusieurs
V pour un même K |
Bidirectional |
|
Conteneurs associatifs sans ordonnancement a priori
Essentiellement, ce sont des tables de hashage
Adaptateurs de conteneurs
Ces « conteneurs » sont en fait des décorateurs paramétriques autour de
conteneurs existants, et offrent une interface spécialisée convenant à leur
nature. Conséquemment, ils n'offrent pas d'itérateurs sur les éléments, car ce
serait contraire à leur vocation.
| Conteneur |
Rôle |
Remarques |
|
stack<T>
|
Implémente une structure de données LIFO
(Last In, First Out) |
Par défaut, le conteneur sous-jacent sera un
deque<T> (ce qui m'a toujours étonné : il me semble que
vector<T>
aurait été plus adéquat, mais bon) |
|
queue<T>
|
Implémente une structure de données FIFO
(First In, First Out) |
Par défaut, le conteneur sous-jacent sera un
deque<T> |
|
priority_queue<T>
|
Implémente une file dont les éléments sont placés en ordre en
fonction d'un prédicat d'ordonnancement paramétrique |
Par défaut, le conteneur sous-jacent sera un
vector<T> et
l'ordonnancement se basera sur
less<T> |
Lectures complémentaires
Un chapitre du livre
../../Liens/Suggestions-lecture.htmll#programming_principles_practice_using_cpp de
Bjarne Stroustrup, mis en ligne en 2014
et expliquant comment utiliser des tableaux et des vecteurs :
http://www.informit.com/articles/article.aspx?p=2216986
Quelques textes d'Andrew Koenig :
Dans la foulée des réflexions d'Andrei
Alexandrescu et de ses travaux sur le langage
D, un
mouvement a été amorcé vers le développement d'algorithmes reposant sur des
intervalles (Ranges) plutôt que sur des itérateurs (sans toutefois
remplacer les itérateurs, qu'ils utilisent généralement de manière
sous-jacente). Ces algorithmes permettent une meilleure composition
d'opérations, et une approche plus près de ce que permet traditionnellement la
programmation fonctionnelle. À ce sujet :
Texte de 2014 par
Bartosz Milewski, pour qui les
intervalles sont une forme de bonbon
monadique :
http://bartoszmilewski.com/2014/10/17/c-ranges-are-pure-monadic-goodness/
Eric Niebler
est celui qui a proposé
ce qui semble être
destiné à devenir la bibliothèque standard d'intervalles en vue de
C++ 20.
Quelques-uns de ses textes sur le sujet :
- À propos des intervalles « comptés », opérant sur un nombre d'éléments, et de
l'efficacité des implémentations, un texte de 2014 :
http://ericniebler.com/2014/10/06/counted-ranges-and-efficiency/
- Des algorithmes pour intervalles, texte de 2014 :
http://ericniebler.com/2014/11/23/container-algorithms/
- Une implémentation de Slices comme on en trouve en
Python,
texte de 2014 :
http://ericniebler.com/2014/12/07/a-slice-of-python-in-c/
- Interaction des concepts avec les
itérateurs menant vers des objets Proxy, comme par exemple ceux
permettant de parcourir un vector<bool>, texte de
2015 :
http://ericniebler.com/2015/01/28/to-be-or-not-to-be-an-iterator/
- Raffiner certaines opérations comme iter_swap()
pour permettre une personnalisation d'opérations de permutation d'éléments
représentés par des objets
Proxy, texte de 2015 :
http://ericniebler.com/2015/02/03/iterators-plus-plus-part-1/
- Définir plus efficacement ce qu'est, ou n'est pas, un itérateur, de manière
à mieux couvrir les itérateurs donnant accès à des objets Proxy, en
2015 :
http://ericniebler.com/2015/02/13/iterators-plus-plus-part-2/
- Faire collaborer les itérateurs sur des objets Proxy
convenablement avec le reste du standard, en 2015 :
http://ericniebler.com/2015/03/03/iterators-plus-plus-part-3
Conteneurs alternatifs :
Spécialiser un algorithme en fonction des caractéristiques de ses paramètres,
texte de Mark Isaacson en 2014 et en 2015 :
Choisir le bon conteneur en fonction des besoins :
En 2017,
Jonathan Boccara discute des questions
de taille et de capacité des conteneurs :
https://www.fluentcpp.com/2017/10/13/size-capacity-stl-containers/
[1]
Le terme objet est à prendre ici au sens large incluant à
la fois les données de types primitifs et les entités plus
complexes que sont les instances de classes.
[2]
... à l'aide d'un tri fusion.
[3] En fait,
un vecteur vide occupe un espace de 16 bytes,
ce qui est effectivement plus gros qu'un tableau géré manuellement
pour lequel on voudrait conserver la taille (disons 4
bytes) et un pointeur au premier élément (4
bytes). La question se pose, cela dit, à savoir si
une perte de 8 bytes par conteneur
est telle qu'on voudrait réécrire la logique toute entière
de prise en charge d'un tableau dynamique et la tester exhaustivement pour
l'amener vers un niveau de performance équivalent.
[4]
...ou l'appel de sous-programme, qui en est l'équivalent
procédural...
[5] Ce remplacement
se fera idéalement à la compilation, pour que le coût
à l'exécution soit nul, mais plusieurs moteurs interprétés
ou semi interprétés comme le
CLR de
.NET et la
JVM de Java
réalisent maintenant une analyse préliminaire du code avant
appel et procèdent à une forme d'inlining dynamique
qui donne dans l'ensemble d'assez bons résultats.
[6]
Évidemment, ceci présume un découpage réalisé
avec soin, des paramètres passés selon un mode soigneusement
choisi (par valeur, par référence, constant ou non, etc.),
des opérations de qualité comparable et ainsi de suite.




