Nombres à virgule flottante

Les équations sur ce site sont affichées avec MathJax.

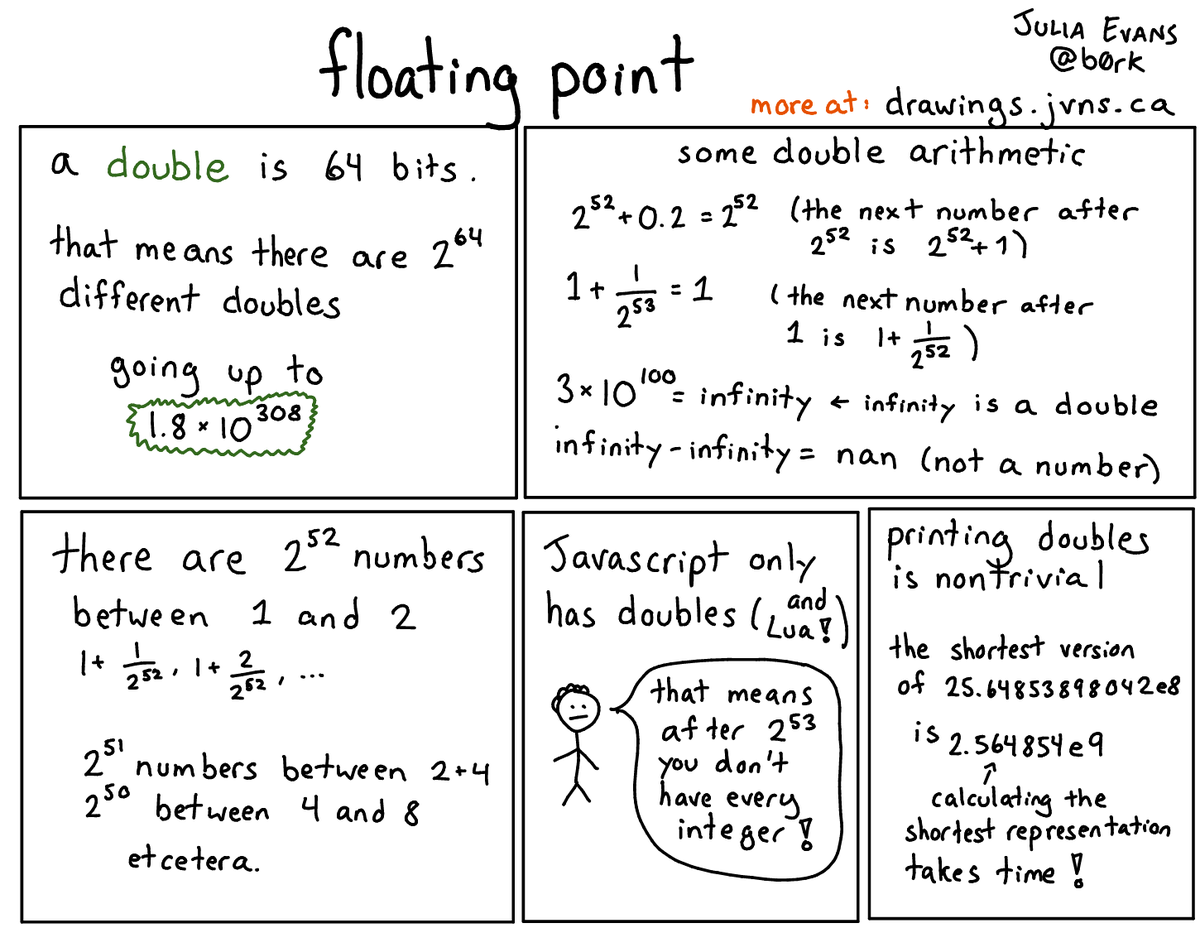
Merci à Julia Evans

Manipuler efficacement et correctement les nombres à virgule flottante est une chose bien plus périlleuse qu'il n'y paraît à première vue, et dont les périls échappent à bien des gens. À ce sujet :

Aussi, quelques articles :

Arrondir un nombre à virgule flottante est un exercice beaucoup plus ardu qu'il n'y paraît à première vue :

À propos des nombres à virgule flottante décimaux :

Dans un texte de 2012 (http://www.drdobbs.com/cpp/are-you-sure-that-your-program-works/240006889 si vous y avez accès), Andrew Koening souligne la difficulté d'écrire des programmes qui sont véritablement corrects, au sens où l'on peut s'en convaincre. Il tient pour exemple une fonction telle que :

double f(double x, double y, double z) {
   return x + y + z;
}

...qui semble tout à fait correcte, mais met en relief qu'un appel de la forme suivante :

// ...
double res = f(1E100,1.0,-1E100);
// ...

...devrait en théorie déposer 1.0 dans res (puisque les valeurs 1E100 et -1E100 s'annulent lorsqu'on les additionne, toujours en théorie) mais qu'il est aussi possible qu'on obtienne 0.0 du fait que l'addition de 1.0 à 1E100 résultera peut-être en 1E100 puisque 1.0 est tout petit et 1E100 est énorme, à un point tel qu'y ajouter 1.0 pourrait ne rien y changer de par la nature même de l'encodage de ces approximations que sont les nombres à virgule flottante. En pratique, il est donc difficile de raisonner sur le caractère correct ou non de cette fonction (en fait, c'est un cas où n'est pas nécessairement égal à , donc où l'addition peut ne pas être commutative; on trouve des cas semblables avec les entiers dans des cas de débordements).

Selon les langages de programmation :

Bien que les nombres à virgule flottante soient maintenant supportés de manière native (matérielle) par la plupart des ordinateurs, et bien que la majorité d'entre eux supportent la même représentation IEEE, ce ne fut pas toujours le cas. Encore aujourd'hui, on a parfois recours à des représentations « maison », typiquement pour de l'arithmétique à point fixe :

À quel point les nombres à virgule flottante sont-ils étranges? Prenez l'exemple suivant (en C++, mais je l'ai adapté d'un exemple en Java et la situation est indépendante du langage) :

#include <iostream>
using namespace std;
int main() {
   int i = 2020202048;
   i += 0.0f;
   cout << i << endl;
}

... qui affichera :

2020202048
2020201984

... ce qui est pour le moins divertissant.

Valid XHTML 1.0 Transitional

CSS Valide !