Structure interne des nombres

En informatique, nous faisons toujours face à des ressources limitées. Un monde idéal où il y a assez d'espace pour écrire un nombre fait d'une infinité de chiffres ne nous appartient pas, sauf en imagination.

Parce que nous sommes contraints à des ressources limitées, nous nous dotons de façons de faire qui en rendent l'utilisation efficace. Dans la présente, nous examinerons brièvement la structure interne des nombres dans un ordinateur, mettant principalement l'accent sur les nombres entiers.

Petit retour sur le passé

« Les nombres, surtout les entiers, on connaît ça ». Nous sommes tellement habitués à une notation décimale qu'on ne fait plus attention, à un moment donné, à ce que l'on représente vraiment par leur écriture.

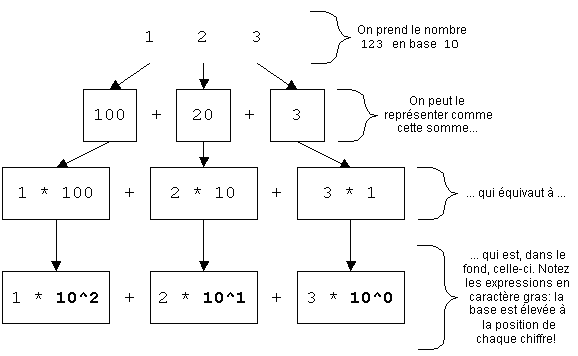
Prenons par exemple l'entier $123$. Nous savons très bien ce que ce nombre signifie : il signifie cent vingt-trois. Et pourtant, il y a d'autres moyens de l'examiner.

Une de ces manières d'examiner ce nombre est plus pertinente à nos fins que d'autres. On peut en effet réécrire $123$ au sens conventionnel de la manière suivante :

Cette forme tient parce que notre système usuel de numérotation est à base décimale (on dit aussi en base $10$). On compose des nombres en disposant des chiffres décimaux de manière à ce que la position de chaque chiffre ait un sens en soi.

Chaque chiffre peut prendre $10$ valeurs distinctes (de $0$ à $9$ inclusivement), d'où les vocables « en base $10$ » et « en notation décimale ». On obtient la valeur d'un nombre en base $10$ en multipliant chaque chiffre par $10$ élevé à la puissance indiquée par sa position, puis en additionnant les valeurs ainsi obtenues.

Exemple : prenons le nombre décimal $4832$. Il peut aussi s'écrire comme suit :

donc :

et par conséquent :

Le chiffre le plus à droite est par convention le moins significatif, et est multiplié par la base ($10$) élevée à la puissance $0$. Le second est multiplié par la base, cette fois élevée à la puissance $1$; le prochain est multiplié par la base élevée à la puissance $2$; etc.

D'autres exemples :

Plusieurs bases possibles

On utilise une base $10$ par habitude. La plupart des humains ont $10$ doigts, $10$ orteils, et il y a un lien entre le choix d'un système à $10$ chiffres et cette réalité.

Mais on pourrait très bien utiliser une autre base que la base $10$, et la mécanique demeurerait la même. L'emploi de la base $10$ n'est rien d'autre qu'une convention, une question d'habitude. Ce n'est pas la seule méthode, la seule base possible.

Choix d'une base et chiffres disponibles

Le choix d'une base indique le nombre de chiffres auxquels on a accès pour écrire un nombre. Quand on utilise la base $10$, on a accès à $10$ chiffres distincts (de $0$ à $9$ inclusivement) pour écrire nos nombres. Si on utilise la base $7$, on aura accès à $7$ chiffres (de $0$ à $6$ inclusivement).

Pour indiquer la base dans laquelle un nombre est rédigé, on indique celle-ci en indice (en bas à droite du nombre en question, écrit en plus petit). Par exemple, $23_4$ signifie « $23$ en base $4$ ». En mathématiques, la plupart du temps, un nombre pour lequel on n'indique pas de base est un nombre décimal.

Exemple d'un nombre écrit dans une autre base que la base $10$

On pourrait utiliser la base $4$, par exemple (les chiffres iraient alors de $0$ à $3$ inclusivement). Dans ce cas, on pourrait écrire le nombre suivant (le petit $_4$ à la fin indique l'emploi de la base $4$) :

en notation décimale, cela nous donnerait (pris de droite à gauche, alors attention!) :

ce qui équivaut à :

donc :

...ce qui équivaut à :

Ainsi, le nombre $10321_4$($10321$ en base $4$) représente la même valeur que le nombre $313_{10}$($313$ en base $10$). Ce sont là deux manières différentes d'écrire la même idée.

Les bases les plus utilisées en informatique

Par habitude, nous – les humains – pensons nos nombres en base $10$. C'est donc le mode par défaut pour interagir avec des humains de plusieurs langages de programmation comme C++.

Le langage C++ utilise par défaut la notation décimale. Pas pour aider l'ordinateur, bien sûr, mais plutôt pour faciliter la vie des humains.

Lorsqu'on compile un programme C++, les opérations que le compilateur y trouve sont traduites en langage machine, et les nombres y sont représentés de manière à faciliter la tâche de l'ordinateur.

Pour un ordinateur, la base $10$ ne serait pas pratique, entre autres parce qu'il faudrait trouver une manière de codifier $10$ chiffres distincts pour implanter des systèmes de numérotation.

Les ordinateurs, si on regarde très près de la machine (à très bas niveau), ne comprennent que la base $2$ – où l'on ne trouve que deux chiffres possibles, $0$ et $1$.

Deux autres bases sont assez communes dans le monde merveilleux de l'informatique, en particulier avec le langage C++. Ce sont les bases $8$ (on parle de nombres en notation octale) et $16$ (nombres en notation hexadécimale).

Nous allons les expliquer brièvement, et montrer comment les exprimer en C++. La notation de C++ est la même que pour C, Java, C# et plusieurs autres langage.

Le chiffre binaire – le bit

L'unité minimale de donnée dans un ordinateur est le bit. Un bit est un chiffre binaire (base $2$), dont la valeur ne peut donc être que $0$ ou $1$, et rien d'autre.

Si on ne prend qu'un seul bit, on ne peut exprimer que deux valeurs distinctes ($0$ et $1$). Si on prend deux bits, on peut exprimer quatre ($2^2$) valeurs distinctes :

avec trois bits, on pourra exprimer huit ($2^3$) valeurs distinctes :

avec quatre bits, on pourra exprimer seize ($2^4$) valeurs distinctes :

et, de manière générale, avec $n$ bits, on pourra alors exprimer $2^n$ valeurs distinctes. Ainsi, avec $8$ bits, on pourra exprimer $2^8$ (donc $256$) valeurs distinctes – que nous n'énumérerons pas.

Puisqu'on considérera qu'un nombre binaire fait entièrement de zéros vaut zéro, on dira que le plus grand nombre possible sur $n$ bits est $2^n-1$. Ainsi, sur $8$ bits, les nombres iront de $0$ à $2^8-1$ (de $0$ à $255$), ce qui donne bien $256$ possibilités.

Exercice : étant donné ce que nous avons vu sur les nombres et les bases, plus haut, exprimez sous forme décimale les nombres binaires ci-dessous :

Des nombres de taille limitée

En mathématiques, les nombres sont souvent idéalisés, pouvant être de précision infinie (pensons à $\pi$ par exemple, qu'on approche de manière aussi précise qu'on le veut).

En informatique, la mémoire disponible est nécessairement limitée, donc les nombres à développement infini ne sont pas envisageables. L'informaticienne et l'informaticien doivent vivre avec ce genre de considération.

De même, les besoins de vitesse font en sorte qu'on travaille presque toujours sur des regroupements d'un certain nombre de bits à la fois – ce nombre est d'ailleurs pratiquement toujours une puissance de deux.

L'octet

Le regroupement le plus petit auquel on ait souvent affaire est l'octet (huit bits). Le charme de l'octet est qu'il permet de représenter $256$ ($2^8$) valeurs distinctes, ce qui permet – entre autres – de couvrir l'étendue des touches du clavier américain.

Les groupes d'octets

On trouve aussi de manière commune des regroupements de $16$ ou de $32$ bits (parfois même de $64$ ou de $128$ bits sur certains ordinateurs haut de gamme), donc de $2$ ou $4$ octets. Il est courant qu'on pense la taille d'un nombre en terme du nombre d'octets qui sont utilisés pour l'encoder.

Pour se donner une idée de ce que ces tailles signifient, examinons un peu :

Pour la plupart des calculs, encore aujourd'hui, des entiers représentés sur $32$ bits suffisent amplement. Les ordinateurs à votre disposition sont généralement bien équipés pour gérer des calculs sur des nombres encodés sur $32$ bits, et de plus en plus d'ordinateurs personnels représentent de manière native des entiers sur $64$ bits.

Entiers

Comment représente-t-on des entiers dans un ordinateur? La première question à se poser est toujours des entiers de quelle taille? (sous-entendu : encodés sur combien de bits?). La seconde est : parle-t-on d'entiers signés ou non signés?

Un entier non signé encodé sur $n$ bits peut prendre des valeurs allant de $0$ à $2^n-1$ (ce qui couvre une plage de $2^n$ valeurs distinctes). Concrètement, un entier non signé sur huit bits peut représenter des valeurs allant de $0$ à $2^8-1$, donc de $0$ à $255$ inclusivement.

Si on regarde la valeur décimale associée aux différents encodages binaires, on verra alors ce que voulez voir à droite.

On voit qu'un encodage de $00000000^2$ vaut précisément zéro; que $00000001^2$ vaut effectivement $1$; que $00000010^2$ équivaut à $2$ (en base $10$); et ainsi de suite, ce qui respecte les règles décrites dans la section sur les bases, plus haut.

Naturellement, $01111111_2$ vaut$127_{10}$ (faites vous-mêmes le calcul pour vous en convaincre : $0 + 64 + 32 + 16 + 8 + 4 + 2 + 1$). Puis, $10000000_2$ vaut $128_{10}$, $10000001_2$ vaut $129_{10}$, etc. jusqu'à $11111111_2$ qui vaut $255_{10}$.

Exercice : les entiers binaires suivants sont des entiers non signés sur $16$ bits. Exprimez chacun sous forme décimale.

Exercice : les entiers décimaux suivants sont des entiers non signés sur $16$ bits. Exprimez chacun sous forme binaire.

Un entier signé encodé sur $n$ bits peut prendre des valeurs allant de $-(2^{n-1})$ à $2^{n-1}-1$ (ce qui couvre encore une fois une plage de $2^n$ valeurs distinctes).

Concrètement, un entier non signé sur huit bits peut représenter des valeurs allant de $-(2^7)$ à $2^7-1$, donc de $-128$ à $127$ inclusivement.

On a choisi d'encoder les valeurs ainsi pour permettre une étendue qui aurait le même nombre de valeurs positives que négatives (considérant, par convention, $0$ comme positif).

Si on regarde la valeur décimale associée aux différents encodages binaires, on verra alors (à droite) :

Dans le cas des entiers signés, relevons que le bit le plus à gauche de la représentation choisie est à $1$ lorsque le nombre est négatif, et qu'il est à $0$ lorsque le nombre est positif. On nomme ce bit bit de signe.

Ce qui diffère donc, au fond, entre un entier non signé et un entier signé, c'est l'interprétation faite d'un seul bit. Aussi, utiliser un bit pour dénoter le signe fait en sorte qu'il y ait exactement la même quantité de nombres positifs et négatifs, peu importe le nombre de bits employés dans la représentation.

Exercice : les entiers binaires suivants sont des entiers signés sur $16$ bits. Exprimez chacun sous forme décimale.

Exercice : les entiers décimaux suivants sont des entiers signés sur $16$ bits. Exprimez chacun sous forme binaire.

Débordements

Si les nombres que nous manipulons ont une taille finie (plutôt qu'infinie), il est possible qu'on provoque, en opérant sur eux, ce qu'on appelle des débordements.

Prenons par exemple un entier non signé sur $8$ bits (valeurs allant donc de $0$ à $255$ inclusivement), et ajoutons-lui $1$.

Si notre entier valait $255$, il vaudra maintenant ... au fait, que vaudra-t-il? Sûrement pas $256$, puisqu'il est impossible d'encoder cette valeur si notre échelle va de $0$ à $255$ inclusivement.

En fait, il vaudra maintenant $0$, et nous aurons causé un débordement. Le terme débordement tient du fait que la capacité de représentation de notre type de données (entier sur $8$ bits non signé) aura été excédée par notre opération.

Un débordement se représente simplement avec une addition, mais peut être causé par toute opération dont le résultat excède les bornes possibles du type de données choisi.

L'idée de débordement peut être représentée à l'aide d'un cercle, autour duquel on trouve les valeurs possibles pour la représentation choisie (ici, on utilise encore les entiers signés sur huit bits, question de garder l'exemple le plus simple possible). L'addition peut être vue comme tourner dans le sens horaire. Vu ainsi, $255+1$ donne effectivement $0$.

Le même phénomène cyclique se produit sur des entiers signés, à la différence près que le débordement ne se produit pas aux mêmes valeurs.

Ici, la frontière entre le plus grand nombre et le plus petit nombre pouvant être représentés est franchie quand on passe de $127$ à $-128$ et inversement. En effet, sur des entiers signés encodés sur huit bits, $127+1=-128$ et $-128-1=127$.

Les exemples donnés ci-dessus l'ont été à l'aide d'entiers sur $8$ bits, mais les idées associées valent pour des entiers de n'importe quelle taille ($16$ bits, $32$ bits, ...), dans la mesure où celle-ci est finie.

Sur $16$ bits, par exemple, la frontière se situe entre $2^{16}-1$ (donc $65535$) et $0$ pour les entiers non signés...	...et entre $2^{15}-1$ ($32767$) et $-(2^{15})$ (donc $-32768$) pour les entiers signés.

Les types entiers en C++

Le langage C++ offre un certain nombre de types de données pour représenter des entiers. Ainsi, on a accès aux types suivants :

Par défaut, ces types sont signés. On peut spécifier le caractère signé en préfixant le type du mot signed. On peut aussi spécifier un entier comme étant non signé par le préfixe unsigned.

Exemples :

// Quelques valeurs approximatives
unsigned int nb_humains;
// approx. 8000000
unsigned short population_CLG; // approx. 5850
// Pour celle ci-dessous, on aurait pu ecrire « short » simplement
signed short fluctuation_compte_bancaire; // c'est un secret!

Exercice : avec ce que l'on sait maintenant, qu'affichera le programme suivant?

#include <iostream>
int main() {
   using namespace std;
   short s;
   s = 32767;
   cout << s << endl;
   s = s + 1;
   cout << s << endl;
}

Notations possibles

En C++, on peut représenter un littéral entier sous trois formes différentes :

• la forme décimale (base $10$);
• la forme octale (base $8$); et
• la forme hexadécimale (base $16$).

Il n'y a pas, à même le langage, de notation binaire. Toutefois, nous le verrons plus bas, il est très simple de passer de la notation hexadécimale à la notation binaire, et inversement.

Notation décimale

La notation décimale est celle, commune, que nous utilisons habituellement sans trop nous poser de questions. Les littéraux $12$, $-34$ et $9876$ sont des littéraux décimaux (base $10$), et ont le sens usuel.

Notation octale

La notation octale débute l'écriture d'un nombre par le chiffre $0$. Ainsi, $07$, $012$ et $0435$ sont tous des nombres écrits en notation octale (leurs équivalents décimaux sont, respectivement, $7$, $10$ et $285$).

Le chiffre $0$ a le même sens en notation octale comme en notation décimale.

Puisque la notation octale (base $8$) n'utilise que des chiffres allant de $0$ à $7$ inclusivement, l'écriture $08$ est illégale ($8$ n'est pas un chiffre valide en notation octale). En base $8$, des nombres comme $093$ ou $011181$ sont illégaux parce qu'ils sont en partie faits de chiffres qui n'y existent pas.

Exercices : Vous trouverez ci-dessous des nombres exprimés sous forme octale, de la manière comprise par le compilateur C++. Exprimez chacun d'entre eux sous forme décimale (non signée) et sous forme binaire[2].

Pourquoi la notation octale?

La notation octale existe en C++ surtout pour des raisons historiques. Le langage C++ s'est inspiré, côté syntaxe, du langage C, très massivement utilisé dans l'industrie, à un tel point qu'en théorie, un compilateur C++ devrait être capable de compiler presque tout programme écrit en langage C.

Le langage C, lui, supportait la norme octale surtout parce qu'il a été développé, à l'origine, sur des ordinateurs qui, eux, utilisaient un format octal pour représenter les opérations très près de la machine.

Ça a un côté pratique: chaque chiffre octal peut prendre huit, donc $2^3$, valeurs différentes. Pour un nombre comme $04312$, on peut donc arriver facilement au nombre binaire correspondant, chaque chiffre octal correspondant précisément à trois bits.

Pour les gens qui programmaient à cette époque, l'aisance avec laquelle on pouvait passer d'un nombre écrit sous forme octale à un nombre écrit sous forme binaire était d'une grande utilité.

Même si elle est beaucoup moins utilisée qu'auparavant, la notation octale mérite d'être mentionnée au passage... Sinon, expliquer pourquoi $09$ n'est pas un nombre deviendrait une tâche fort difficile.

Notation hexadécimale

La notation hexadécimale débute l'écriture d'un nombre par $0x$. Ainsi, $0x7$, $0x12$ et $0x435$ sont tous des nombres écrits en notation hexadécimale (leurs équivalents décimaux sont, respectivement, $7$, $18$ et $1077$).

Le chiffre $0x0$ a le même sens que le $0$ en notation octale ou décimale.

Puisque la notation hexadécimale (base $16$ ) nécessite $16$ chiffres distincts, on utilise les chiffres allant de $0$ à $9$ inclusivement de même que les lettres $a$ à $f$ ( $a$ valant $10$ en notation décimale, et $f$ valant $15_{10}$ ). Ces « lettres » peuvent s'écrire en majuscules ou en minuscules, à votre convenance (j'utiliserai les minuscules ici).

Ainsi, l'écriture $0a$ est illégale ($a$ n'est pas un chiffre valide en notation octale), et l'écriture $fc$ n'est pas un nombre. En revanche, les écritures $0xa$ et $0xfc$ sont tout à fait légales.

Exercices : Vous trouverez ci-dessous des nombres exprimés sous forme hexadécimale, de la manière comprise par le compilateur C++. Exprimez chacun d'entre eux sous forme décimale (non signée) et sous forme binaire[3].

Pourquoi la notation hexadécimale?

La notation hexadécimale existe en C++ pour des raisons analogues à celles justifiant l'écriture octale (voir ci-dessus). Contrairement à l'écriture octale, quelque peu désuète, l'écriture hexadécimale est encore fort utilisée.

En effet, chaque chiffre hexadécimal peut prendre seize ($2^4$) valeurs différentes. Pour un nombre comme $0xf03c$ , on peut donc arriver facilement au nombre binaire correspondant, chaque chiffre hexadécimal correspondant précisément à quatre bits (on nomme parfois nybble un bloc de quatre bits) – conséquemment, un octet est représenté par un nombre hexadécimal de deux chiffres.

Nombres à virgule flottante (ce qui tient lieu de réels)

Les réels, tout comme les entiers, sont encodés à l'aide de bits. Il y a par contre plus de standards différents pour procéder à cet encodage. Un d'entre eux (une norme IEEE) est plus répandu que les autres, et nous en dresserons l'idée ici.

Au niveau binaire, on manipule beaucoup plus rarement des réels que des entiers. S'il importe de comprendre l'idée de l'encodage, en maîtriser la forme est moins important – si vous en avez un jour besoin, ce qui est improbable, vous pourrez vous référer à la norme elle-même, qui est disponible dans Internet[4].

La représentation des réels est dite à virgule flottante. On nomme ces nombres des nombres à virgule flottante.

Les nombres à virgule flottante ne sont pas représentés en mémoire de la même façon que les entiers, ce qui comporte son lot d'avantages et de désavantages. Leur représentation interne se compose de trois parties : le signe, l'exposant et la mantisse.

Comme dans le cas des entiers, le signe est représenté par un bit unique ($1$ pour les nombres négatifs, $0$ pour les nombres positifs), qui est normalement le bit le plus à gauche dans la représentation du nombre.

On lit ces valeurs comme suit :

Selon le nombre de bits utilisés pour représenter un nombre à virgule flottante, la taille de l'exposant et de la mantisse varieront – pour le signe, un bit est toujours suffisant.

Il n'y a pas de nombres à virgule flottante non signés. Le signe fait partie intégrante de toutes les représentations standard.

L'exposant sera un entier pouvant être positif ou négatif. La mantisse sera une fraction exprimée sous forme décimale, toujours entre $1$ et $2$.

Un nombre à virgule flottante permet en général de représenter une approximation d'un nombre réel. Plus sa mantisse et son exposant sont grands, plus la plage de valeurs possibles est grande, et il en va de même pour la précision des valeurs représentées. C'est, à peu de choses près, ce qu'il faut en retenir.

Les types à virgule flottante en C++

Le langage C++ offre un certain nombre de types de données pour représenter des nombres à virgule flottante. Ainsi, on a accès aux types suivants :

Ces types sont tous signés.

Prudence

Quand nous programmons, nous devons être conscientes et conscients de ces détails techniques, puisqu'ils ont une influence sur la qualité de nos résultats. Un débordement non désiré est souvent une erreur de logique; une manipulation inadéquate d'un nombre réel peut mener à une variété de problèmes et d'assertions erronées – nous y reviendrons.

Conséquemment, le choix du mauvais type de données peut avoir des conséquences allant de mineures (un résultat incorrect dans un travail pratique dans un cours d'introduction à la programmation) à très graves (une erreur dans le calcul de la trajectoire d'un projectile).

Lecture complémentaire

Quelques liens pour enrichir le propos.

• En 2015, Paul Watt explique les systèmes positionnels de numération :
  • http://codeofthedamned.com/index.php/number-base-conversion
  • http://codeofthedamned.com/index.php/learn-hexadecimal-and-binary
• Série de textes par Cédric Bellet, et portant sur les opérations bit à bit :
  • introduction : https://medium.com/biffures/launching-bitwise-bits-from-the-ground-up-9565303caf13
  • conventions de nommage : https://medium.com/biffures/bits-101-120f75aeb75a
  • à propos de la beauté des opérateurs « et » bit à bit : https://medium.com/biffures/part-2-the-beauty-of-bitwise-and-or-cdf1d8d87891

[1] La taille indiquée vaut pour plusieurs compilateurs, mais pas nécessairement pour tous les compilateurs. Certaines règles s'appliquent d'une plateforme à l'autre, mais les tailles elles-mêmes peuvent varier en fonction du compilateur ou de l'ordinateur. Voir cet article pour plus de détails.

[2] Indice : il y a un truc dans la section Pourquoi la notation octale? pour faciliter la traduction de la forme octale à la forme binaire.

[3] Indice : il y a un truc dans la section Pourquoi la notation hexadécimale? pour faciliter la traduction de la forme hexadécimale à la forme binaire.

[4] Entre autres : http://docs.sun.com/source/806-3568/ncg_goldberg.html.

[5] Voir remarque pour les entiers, plus haut.