Comprendre la récursivité

Il y a des sujets qui, pour d'étranges raisons, font plus peur que d'autres. Les pointeurs, par exemple, ou encore le polymorphisme, qui sont des exemples classiques de concepts essentiels en informatique et qui semblent entourés d'une aura de crainte, crainte somme toute peu justifiée.

Le présent document s'intéressera à l'un de ces sujets à haute teneur en crainte : la récursivité.

Un exemple simple... presque simpliste

Imaginons que nous ayons le mandat suivant :

La plupart des informaticiennes et des informaticiens auront sans doute le réflexe de résoudre ce problème à l'aide d'une répétitive, ce qui est une stratégie très raisonnable :

long somme_un_a(int n) {
   long cumul = {};
   for (int i = 1; i <= n; i++)
      cumul += i;
   return cumul;
}

long somme_un_a(int n) {
   long cumul = {};
   int i = 1;
   while (i <= n) {
      cumul += i;
      i++;
   }
   return cumul;
}

On pourrait aussi définir cette fonction de la manière suivante :

long somme_un_a(int n) {
   if (n <= 0)
      return 0L;
   else
      return n + somme_un_a(n-1);
}

Les versions avec répétitives sont plus efficaces dans ce cas-ci, mais la version où la fonction résout le problème en se rappelant elle-même a le mérite d'être très simple :

• On définit un cas d'arrêt: la somme de $1$ à zéro ou moins est zéro, ce que nous savons de par la définition du problème donnée plus haut. Simple, efficace, sans équivoque et – surtout – sans récursivité, et
• On définit un ou plusieurs cas généraux qui s'expriment par une simplification du problème original : ici, $\sum\limits_1^n$ (présumant $n \gt 0$) vaut $n+ \sum\limits_1^{n-1}$ )

La stratégie d'ensemble d'une fonction récursive y est claire :

• Règle générale, on essaie d'exprimer la solution à un problème en fonction de lui même, mais en le simplifiant de manière à ce que, à chaque étape, on converge de plus en plus vers un cas trivial (plus haut, le cas où $n \le 0$), et
• On définit un cas banal qui sera éventuellement atteint et pour lequel la réponse est connue. Sans un tel cas, la récursivité procédera ad infinitum et nous n'aurons pas de solution au problème attaqué

Les fonctions récursives sont l'enfant chéri des mathématicien(ne)s; il est fréquent que des structures mathématiques soient définies de manière récursive, ce qui est compréhensible: règle générale, une stratégie récursive s'exprime de manière simple, élégante et compacte.

succ(0) == 1
succ(1) == succ(succ(0)) == 2
...
succ(n) == succ(succ(n-1))

On peut tracer rapidement ce que cette stratégie donnerait pour $n=5$ lors de l'invocation initiale de somme_un_a() :

somme_un_a(5) == 5 + somme_un_a(4)
            == 5 + (4 + somme_un_a(3))
            == 5 + (4 + (3 + somme_un_a(2)))
            == 5 + (4 + (3 + (2 + somme_un_a(1))))
            == 5 + (4 + (3 + (2 + (1 + somme_un_a(0)))))
            == 5 + (4 + (3 + (2 + (1 + (0)))))
            == 5 + (4 + (3 + (2 + (1))))
            == 5 + (4 + (3 + (3)))
            == 5 + (4 + (6))
            == 5 + (10)
            == 15

Remarquez que la solution du problème résulte d'un cumul de données. La stratégie récursive repousse à la toute fin de la récursion la tâche de mettre ensemble les petits morceaux de calculs trouvés en chemin.

Cela a pour effet qu'une fonction récursive requiert, en général, des ressources cumulatives pour en arriver à un résultat, quand bien même ce ne serait que pour gérer les appels à la fonction récursive qui s'empilent jusqu'à obtention d'un résultat: somme_un_a(5) ne peut se compléter sans avoir obtenu le résultat de somme_un_a(4), qui dépend du résultat de somme_un_a(3), et ainsi de suite, ce qui fait en sorte que somme_un_a(n) entraînera, au pire moment, $n$ (en fait, $n+1$, mais cela importe peu) appels empilés à somme_un_a().

Chaque appel entraîne l'utilisation d'espace pour les états intermédiaires (valeur de retour, variables locales, etc.) ce qui peut devenir très, très coûteux :

Dans le schéma qui précède, en forme de pyramide, le pic de la pyramide représente le moment où on a atteint le coût maximal en ressources pour un appel original à somme_un_a(5). On imagine bien le coût de somme_un_a(10000), surtout en comparaison avec une stratégie itérative qui ne ferait que $10000$ itérations dans une répétitive et qui, en ne se rappelant pas, ne nécessiterait qu'un seul appel à la fonction somme_un_a().

long somme_un_a(int n) {
   long cumul = {};
   if (n > 0)
      if (n % 2 == 0) // n pair
         cumul = (1 + n) * (n / 2);
      else
         cumul = n + (1 + (n - 1)) * ((n-1) / 2);
   return cumul;
}

long somme_un_a(int n) {
   if (n <= 0)
      return 0L;
   else if (n % 2 == 0) // n pair
      return (1 + n) * (n / 2);
   else
      return n + somme_un_a(n-1);
}

Cas où la stratégie récursive est avantageuse

Imaginons que nous ayons le mandat suivant :

Ici encore. une solution répétitive est très accessible – il s'agit même d'un problème fréquemment servi à des étudiant(e)s inscrit(e)s dans un cours de base de programmation :

long puissance(int base, int exp) {
   long cumul = 1L;
   for (int i = 0; i < exp; ++i)
      cumul *= base;
   return cumul;
}

long puissance(int base, int exp) {
   long cumul = 1L;
   int cpt = 0;
   while (cpt < exp) {
      cumul *= base;
      ++cpt;
   }
   return cumul;
}

On pourrait aussi définir cette fonction de la manière suivante, qui est simple et relativement inefficace, à l'image de la version récursive de somme_un_a() plus haut.

long puissance(int base, int exp) {
   if (!exp)
      return 1L;
   else
      return base * puissance(base, exp - 1);
}

Pour se le prouver, traçons l'appel puissance(2,5) :

puissance(2,5) == 5 * puissance(2,4)
               == 5 * (4 * puissance(2,3))
               == 5 * (4 * (3 * puissance(2,2)))
               == 5 * (4 * (3 * (2 * puissance(2,1))))
               == 5 * (4 * (3 * (2 * (1 * puissance(2,0)))))
               == 5 * (4 * (3 * (2 * (1 * 1))))
               == 5 * (4 * (3 * (2 * (1))))
               == 5 * (4 * (3 * (2)))
               == 5 * (4 * (6))
               == 5 * (24)
               == 120

mais ce n'est pas la seule manière possible de procéder. Une analyse plus poussée du problème révèle des trucs amusants : en effet, il se trouve que si exp est pair, alors exp peut s'écrire sous la forme $2 \times n$ avec $n$ entier. On sait alors que :

baseexp == base2*n
        == basen+n
        == basen*basen
        ==(basen)2

On voit donc poindre à l'horizon une forme de récursivité beaucoup plus intéressante: lorsque exp est pair, on peut évaluer base^exp en calculant base^exp/2 et en multipliant cette valeur par elle-même, diminuant ainsi de moitié la complexité du problème!

Évidemment, si exp est impair, on aura recours à la version plus simple qui consiste à calculer base*puissance(base,exp-1).

Cette version plus efficace pourrait se présenter comme suit :

bool est_pair(int n) {
   return n % 2 == 0;
}
long puissance(int base, int exp) {
   if (exp == 0)
      return 1L;
   else if (est_pair(exp)) {
      auto temp = puissance(base,exp/2);
      return temp * temp;
   } else
      return base * puissance(base, exp - 1);
}

puissance(base,exp/2) == puissance(base,0)

Pour visualiser l'impact de cette manoeuvre, traçons l'appel puissance(2,10). Nous utiliserons n^2 pour signaler l'élévation au carré de n, en présumant qu'il s'agit d'une opération primitive puisque, dans la fonction, nous utilisons une variable temporaire qu'on multiplie par elle-même pour réaliser cette opération (donc on ne procède par récusivement) :

puissance(2,10) == puissance(2,5)^2
                == (2 * (puissance(2,4))^2
                == (2 * puissance(2,2)^2)^2
                == (2 * (puissance(2,1)^2)^2)^2
                == (2 * ((2*puissance(2,0))^2)^2)^2
                == (2 * ((2*1)^2)^2)^2
                == (2 * (2^2)^2)^2
                == (2 * 4^2)^2
                == (2 * 16)^2
                == (32)^2
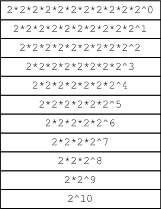
                == 1024

Il peut être intéressant de comparer la stratégie récursive naïve avec celle-ci pour voir la différence de complexité entre les deux approches. Visuellement, les pire cas (en terme de récursivité) des deux approches se présentent, pour puissance(2,10), comme suit.

La notation 2^n a été préférée à la notation puissance(2,n) dans ces schémas pour économiser de l'espace, mais n'oubliez pas que, dans la stratégie de droite, l'opération n^2 est une opération primitive (se fait sans récursivité) dans tous les cas sauf un (en gras et en italiques) qui constitue un légitime appel à puissance(2,2).

puissance(2,10), pire cas
Algorithme naïf	Algorithme plus raffiné

Ne nous y méprenons pas: si la différence est visible avec exp==10, elle ira en s'accroissant alors que exp croîtra. Notez que cette assertion doit être vérifiée (il y a des algorithmes efficaces sur de petits problèmes mais beaucoup moins efficaces sur de grands problèmes), mais est véridique dans ce cas-ci.

C'est un indice important dans le choix d'un algorithme: plus la taille du problème est grande et plus l'écart se creuse entre un bon algorithme et un moins bon.

On fait souvent appel à l'informatique pour résoudre des problèmes que des humains ne pourraient pas raisonnablement résoudre sans outils. Des problèmes demandant beaucoup de calculs, par exemple; le tri de vastes quantités de données; des problèmes où le nombre d'opérations est tel que la force brute devient nécessaire; etc. Les gains apportés par l'emploi de bons algorithmes sont, dans la majorité des cas, beaucoup plus importants que ceux apportés par l'usage d'un ordinateur plus puissant.

Clairement, dans ce cas-ci, la récursivité, bien appliquée, nous permet de concevoir un algorithme beaucoup plus efficace que l'algorithme récursif naïf ou que l'algorithme itératif (avec une boucle), dont la complexité est linéaire (le nombre d'itérations requis pour calculer puissance(base,exp) suit de manière linéaire la valeur de exp).

Visiblement, la récursivité n'est pas la solution à tous les maux, mais peut être un outil conceptuel de grande valeur.

Vieux truc scout : valider à moindre coût le respect des invariants primitifs

Comment pourrait-on écrire la fonction puissance(base,exp) de manière à ce que :

• cette fonction valide elle-même le respect des invariants que sont base > 0 et exp >= 0 (levant une exception si ces invariants ne sont pas respectés);
• cette validation ne soit faite qu'une seule fois, lors de l'appel initial, de manière à ne pas entraîner de perte de performance à chaque fois que la fonction se rappellera elle-même; et
• les utilisateurs de la fonction n'y voient que du feu?

Une manière simple d'y arriver est d'appliquer une façade de validation : la fonction ayant la signature attendue (ici : puissance(base,exp)) est exposée (dans un fichier d'en-tête) est sera appelée par le sous-programme utilisateur. Notez que vous trouverez des informations sur les templates dans cet article.

#include <string>
#include <sstream>
//
// Ce qui suit est discutable, mais suffira pour cet article
//
template <class T>
   struct ParametreInvalide {
      std::string nom;
      T valeur;
      std::string message() const  {
         return "Paramètre invalide: (" + nom + "): " + to_string(valeur);
      }
      ParametreInvalide(const std::string &nom, const T &val) : nom{ nom }, valeur{ val }  {
      }
   };
//
// Prototype de la fonction
//
long puissance(int base, int exp);

Toutefois, cette fonction n'est qu'une façade, qui procède à une validation unique des paramètres. Pour son traitement, elle fait appel à une autre fonction qui, elle, n'est pas exposée (qui est cachée dans un .cpp), et c'est cette fonction cachée qui, confiante que ses paramètres respectent les invariants attendus, procédera pleine valeur et récursivement sans les valider.

La même technique s'appliquerait dans une stratégie OO en utilisant une méthode publique comme façade de validation et une méthode privée pour la version rapide mais sans validation pour le calcul brut.

Dans notre exemple, puissance(base,exp) est la façade qui procède à la validation du respect des invariants par les paramètres base et exp, et ::puissance_impl(base,exp) fait le réel travail pour calculer l'élévation de base à la puissance exp.

Procédant ainsi, ::puissance_impl(base,exp) peut déployer au maximum sa puissance de calcul et puissance(base,exp) offre aux sous-programmes utilisateurs la sécurité à laquelle ils sont en droit de s'attendre. Plus exp est grand et moins la façade sera coûteuse.

// inclure le fichier d'en-tête...
namespace {
   //
   // est_pair(n), simple et efficace
   //
   bool est_pair(int n) {
      return n % 2 == 0;
   }
   //
   // Fonction brute, usage interne seulement, paramètres
   // présumés préalablement validés
   //
   long puissance_impl(int base, int exp) {
      if (exp == 0)
         return 1L;
      else if(est_pair(exp)) {
         auto temp = puissance_impl(base,exp/2);
         return temp * temp;
      } else
         return base * puissance_impl(base, exp - 1);
   }
}
//
// Définition de la fonction façade
//
long puissance(int base, int exp) {
   if (base <= 0)
      throw ParametreInvalide<int>("Base", base);
   else if (exp < 0)
      throw ParametreInvalide<int>("Exp", exp);
   return ::puissance_impl(base, exp);
}

Variante – expression λ récursive et std::function

Une variante plus concise de la stratégie précédente est d'avoir recours à une expression λ interne à la fonction servant de façade. Le code suit :

// inclure les fichiers d'en-tête...
bool est_pair(int n) {
   return n % 2 == 0;
}
//
// Définition de la fonction façade
//
long puissance(int base, int exp) {
   if (base <= 0)
      throw ParametreInvalide<int>("Base", base);
   else if (exp < 0)
      throw ParametreInvalide<int>("Exp", exp);
   function<long(int,int)> impl = [&](int base, int exp) -> long {
      if (exp == 0)
         return 1L;
      else if(est_pair(exp)) {
         auto temp = puissance_impl(base,exp/2);
         return temp * temp;
      } else
         return base * puissance_impl(base, exp - 1);
   };
   return impl(base, exp);
}

Ici, l'expression λ est logée dans une std::function de manière à être nommée, puis ce nom est capturé par référence dans la λ pour y être utilisé comme une opération récursive. Cette opération est efficace du fait que ses paramètres sont nécessairement valides.

Cas où la stratégie récursive est élégante mais très coûteuse

Il existe des cas où la stratégie récursive brute est la plus élégante mais entraîne des coûts considérables. L'un des cas les plus étudiés en ce sens est l'algorithme de Fibonacci, qui décrit entre autres la croissance de certaines plantes et de certaines populations animales.

Cette fonction prend un seul paramètre, un entier naturel $n \ge 0$, et sera nommée fib(n) ci-après.

Son expression naturelle en mathématiques est récursive :

L'écriture récursive de fib(n) va de soi à partir de la définition (on pourrait la garnir d'une façade pour assurer $n \ge 0$, mais nous omettrons ce détail ici pour garder le tout simple) :

long fib(int n) {
   if (n < 2) // ou if (n == 0 || n == 1)
      return 1L;
   else
      return fib(n-1) + fib(n-2);
}

Cette version fonctionne bien, d'ailleurs, mais est terriblement lente pour de grandes valeurs de n. Pour comprendre le problème, traçons l'appel à fib(7) :

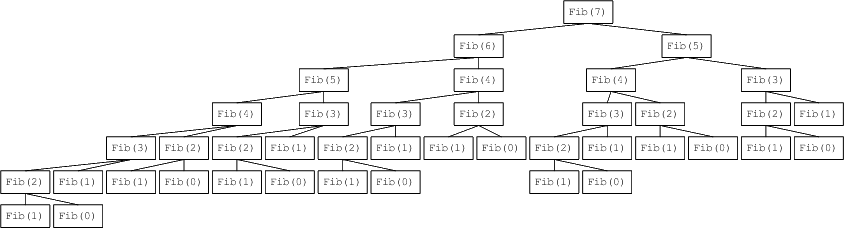
Ce qu'on doit remarquer ici pourcomprendre le problème, c'est à quel point les calculs redondants y sont nombreux. Par exemple, fib(3) y est calculé pas moins de cinq fois, et implique à lui seul le calcul de fib(2), de fib(1) (deux fois!) et de fib(0). On a peine à imaginer la complexité d'un calcul comme fib(25) fait de manière aussi naïve!

Idéalement, on ne calculerait chaque valeur $n$ de fib(n) qu'une seule fois, et on réutiliserait cette valeur chaque fois qu'on en aurait besoin, car chaque calcul de fib(n) pour une valeur de n donnée résulte en une arborescence de calculs. Prenons par exemple fib(5), du côté droit et du côté gauche de l'arborescence ci-dessus: si on avait retenu sa valeur la première fois que celle-ci aurait dû être calculée, alors l'un des deux arbres aurait pu être omis en totalité!

Une version itérative de fib(n) tenant compte de cette réalisation utiliserait un grand tableau. Ici, nous utiliserons new pour le créer et delete pour le détruire, mais si le calcul rapide de fib(n) était important dans un programme, alors on privilégierait l'emploi d'un gros tableau (au moins autant d'éléments que le plus gros n susceptible d'être passé en paramètre à fib()) alloué à l'avance, car l'allocation dynamique de mémoire est une opération coûteuse.

#include <memory>
// Présume n >= 0
long fib(int n) {
   using std::unique_ptr;
   // Cas dégénérés
   if (n < 2) return 1L;
   // Créer un tableau pour entreposer les n valeurs de fib(n)
   unique_ptr<long[]> p { new long[n+1] };
   // Initialiser le tableau
   p[0] = p[1] = 1L;
   // Calculer fib(i) pour i dans (2..n) sans récursivité;
   // chaque valeur n'est calculée qu'une seule fois
   for (int i = 2; i <= n; ++i)
      p[i] = p[i-1] + p[i-2];
   // Le résultat du calcul est en position n du tableau
   return p[n];
}

#include <vector>
// Présume n >= 0
long fib(int n) {
   using std::vector;
   // Cas dégénérés
   if (n < 2) return 1L;
   // Créer un tableau pour entreposer les n valeurs de fib(n)
   vector<long> v(n+1);
   // Initialiser le vecteur
   v[0] = v[1] = 1L;
   // Calculer fib(i) pour i dans (2..n) sans récursivité
   for (int i = 2; i <= n; ++i)
      v[i] = v[i-1] + v[i-2];
   // Le résultat du calcul est en position n du vecteur
   return v[n];
}

Notez que pour la version itérative de fib(n) pour une valeur de n donnée, le recours à un conteneur est abusif; conserver les deux plus récentes valeurs de fib() suffit en tout temps. L'allocation dynamique de ressources qu'implique le recours à un tableau ou à un vecteur tendra, en pratique, à prendre beaucoup plus de temps que les deux affectations supplémentaires par itération dans le code ci-dessous :

// Présume n >= 0
long fib(int n) {
   // Cas dégénérés
   if (n < 2) return 1L;
   // deux plus récentes valeurs évaluées
   long fibA = 1L, fibB = 1L;
   // Calculer fib(i) pour i dans (2..n) sans récursivité
   long fib;
   for (int i = 2; i <= n; i++) {
      // évaluer fib(i)
      fib = fibA + fibB;
      // conserver fib(i-1) et fib(i-2)
      fibA = fibB;
      fibB = fib;
   }
   // bingo!
   return fib;
}

Définir fib(n) de manière récursive est clair et élégant. Implémenter fib(n) de manière récursive, par contre, n'est pas une démarche pragmatique.

Cas où la stratégie récursive est intéressante

struct Noeud {
   int valeur;
   Noeud *succ {};
public:
   Noeud(int valeur) : valeur{valeur} {
   }
   Noeud(const Noeud &n) : val{ n.valeur() } {
   }
};
class Liste {
   Noeud *tete {};
public:
   Liste()= default;
   void ajouter(int n) {
      auto p = new Noeud{ n };
      if (!empty())
         p->succ = tete;
      tete = p;
   }
   bool empty() const {
      return !tete;
   }
   int size() const;
   void afficher_elements() const;
   void afficher_elements_inverse() const;
   void clear() {
      for (auto p = tete; p; ) {
         auto q = p->succ;
         delete p;
         p = q;
      }
      tete = {};
   }
   // etc.
};

Imaginons qu'on ait une liste simplement chaînée définie comme suit (à droite). Il est évidemment possible de faire beaucoup mieux.

Chaque instance de Noeud possède une valeur (constante) et connaît son successeur (un autre Noeud, ou nullptr si elle n'a pas de successeur).

Une liste a une tête (un Noeud). Elle est considérée vide si sa tête est un pointeur nul. On peut ajouter à la liste (l'ajout se fait en début de liste, pour fins de simplicité).

Trois des opérations qui sont déclarées dans cette classe Liste ne sont pas encore définies. Il s'agit de :

• La méthode size(), qui comptera puis retournera le nombre de noeuds dans la liste (on s'attend à $0$ si la liste est vide). On pourrait rendre cette opérations beaucoup plus rapide en insérant un attribut d'instance dans Liste pour tenir à jour le nombre d'instances de Noeud qui y sont répertoriées (en incrémentant le compte à chaque ajout), mais nous omettrons cette optimisation dans ce cas-ci et nous conserverons l'algorithme de complexité linéaire (libre à vous de raffiner le tout)
• La méthode afficher_elements(), qui affichera la valeur de chaque Noeud dans l'ordre où ceux-ci se trouvent dans la liste (ce qui ne correspond pas à l'ordre d'insertion), et
• La méthode afficher_elements_inverse(), qui affichera la valeur de chaque Noeud dans l'ordre inverse de celui où ces instances de Noeud se trouvent dans la liste.

Nous présenterons des implémentations possibles pour ces trois méthodes, et nous examinerons l'utilité (ou non) d'une stratégie récursive dans chaque cas.

Implémenter Liste::size() const

En l'absence d'un compteur toujours à jour pour le nombre d'éléments dans la liste, la manière la plus simple de calculer ce nombre d'éléments est de parcourir cette liste à partir de sa tête jusqu'à ce qu'on atteigne un noeud qui n'ait pas de successeur et de les compter, tout simplement. Dans la version récursive, Liste::size() const sert de façade à une fonction plus générique.

int Liste::size() const {
   int n = {};
   for(auto p = tete; p; p = p->succ)
      ++n;
   return n;
}

private:
   int compter_elements(Noeud *p) {
      if (p)
         return 1 + compter_elements(p->succ);
      else
         return 0;
   }
public:
   int Liste::size() const {
      return compter_elements(tete);
   }

private:
   int compter_elements(Noeud *p) {
      return p? 1 + compter_elements(p->succ) : 0;
   }
public:
   int Liste::size() const {
      return compter_elements(tete);
   }

Visiblement, les deux versions sont aussi complexes l'une que l'autre. Dans un tel cas, on privilégiera presque toujours l'approche itérative, qui nécessite un nombre constant (un seul!) d'appels de méthode, à l'approche récursive, qui exige un nombre d'appels de méthodes qui croît de manière linéaire avec le nombre d'éléments dans la liste.

Implémenter Liste::afficher_elements() const

Encore une fois, il faudra parcourir la liste élément par élément pour afficher la valeur de chacun. Dans la version récursive, Liste::afficher_elements() const sert de façade à une fonction plus générique.

void Liste::afficher_elements() const {
   for(auto p = tete_; p; p = p->succ)
      cout << p->valeur << ' ';
}

private:
   void aff_elems(Noeud *p) {
      if (p) {
         cout << p->valeur;
         aff_elems(p->succ);
      }
   }
public:
   void Liste::afficher_elements() const {
      aff_elems(tete);
   }

Encore une fois, les deux versions sont aussi complexes l'une que l'autre, et on privilégiera l'approche itérative.

Implémenter Liste::afficher_elements_inverse() const

Ici, par contre, une version itérative serait relativement complexe à implémenter :

• Devrait-on se construire une liste temporaire avec des copies de chaque Noeud dans la liste originale mais insérés en ordre inverse de leur ordre dans la liste originale, puis afficher cette liste temporaire, puis la détruire? C'est une stratégie qui demande beaucoup de manipulations et qui est porteuse d'un coût en mémoire
• Devrait-on parcourir la liste originale plusieurs fois, se souvenir du dernier Noeud affiché, et afficher chaque fois celui qui le précède? C'est une stratégie très lourde algorithmiquement (complexité quadratique : pour $n$ éléments dans la liste, on parle de quelque chose se trouvant aux alentours de $\frac{1}{2} \times n^2$ opérations)
• Autre chose d'ésotérique?

La stratégie récursive, elle, est toute simple et sa complexité est linéaire. Ici, Liste::afficher_elements_inverse() const sert de façade à une fonction plus générique

void Liste::afficher_elements_inverse() const {
   // coûte cher en mémoire!
   Liste temp;
   for (auto p = tete; p; p = p->succ)
      temp.ajouter(p->valeur);
   temp.afficher_elements();
}

void aff_inverse(Noeud *p) {
   if (p) {
      aff_inverse(p->succ);
      cout << p->valeur;
   }
}
void Liste::afficher_elements_inverse() const {
   aff_inverse(tete);
}

void Liste::afficher_elements_inverse() const {
   if (!empty()) {
      Noeud *dernier = nullptr;
      do {
         auto p = tete;
         while (p->succ != dernier)
            p = p->succ;
         cout << p->valeur;
         dernier = p;
      }
      while (dernier != tete);
   }
}

Clairement ici, la complexité et la clarté de la version récursive constituent des atouts importants sur leur contrepartie itérative. Dans ce cas, la version récursive serait celle qu'on souhaiterait implémenter.

Cas où on ne voudrait pas se passer de récursivité

Les compilateurs (et les calculatrices!) ont souvent à analyser des expressions mathématiques, comme par exemple :

• L'expression $3$
• L'expression $3 \times 5 + 2$
• L'expression $2 + 3 \times 5$
• L'expression $2 \times (3+5)$
• L'expression $3 \times (2-7) / (3+5)$ , etc.

Ces expressions doivent pouvoir être représentées et évaluées efficacement par un compilateur (ou par un programme tout court), de manière à ce que les priorités des opérateurs et les parenthèses soient respectées.

L'une des manières les plus répandues de représenter ces expressions est sous forme d'arbres. Sans entrer dans les détails (ce serait un peu lourd pour une discussion sur la récursivité) :

• Un arbre est constitué d'une noeud qu'on nomme racine qui possède un nombre $\ge 0$ de noeuds qui sont ses enfants
• Un noeud sans enfant est une feuille
• Chaque noeud enfant est lui-même un arbre – la définition d'un arbre est naturellement récursive, et sa condition d'arrêt repose sur le concept de feuille, ce que nous pourrons vérifier dans nos algorithmes un peu plus bas
• Un arbre ne contient pas de cycles. Prenant par convention que la racine se trouve en haut de l'arbre – les arbres, en informatiques, poussent de haut en bas – cela signifie que tous les traits vont de haut en bas
• Une branche d'un arbre mène de sa racine à l'une de ses feuilles;
• On nomme parfois sommets les noeuds et arêtes les liens entre les noeuds

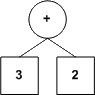
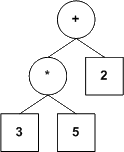
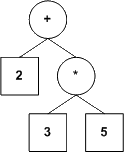
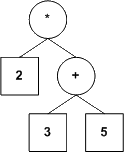
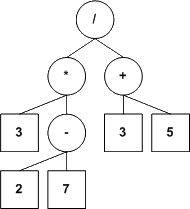
Dans nos arbres, une feuille contiendra une valeur numérique et tout noeud qui n'est pas une feuille contiendra un opérateur (nos opérateurs seront tous binaires, mais ce n'est pas une exigence du modèle; nous voulons simplement garder le tout le plus simple possible).

Voici ce dont pourraient avoir l'air les représentations en arbre des expressions arithmétiques proposées plus haut.

Expression	$3$	$3+2$	$3 \times 5+2$	$2+3 \times 5$	$2 \times (3+5)$	$3 \times (2-7)/(3+5)$
Arbre correspondant

Un algorithme récursif est la manière la plus naturelle d'explorer de telles structures. Pour en faire la démonstration, examinons la méthode valeur() de la classe Noeud ci-dessous, en tenant compte que :

• la classe Noeud sert de base pour les concepts de noeud et de feuille;
• la classe NoeudValeur représente une feuille ayant une valeur fixée à la construction. Sa méthode valeur() se limite à retourner ladite valeur. Tel que prévu, cette classe représente la fin de l'exploration récursive d'une branche d'un arbre;
• la classe NoeudOperateurBinaire implémente le concept de validité d'un noeud représentant un opérateur binaire; et
• les classes NoeudSomme, NoeudDifference, NoeudProduit et NoeudQuotient représentent tous des opérateurs binaires. La méthode valeur() de chaque instance de chacune de ces classes est implémentée par une exploration récursive des arbres constitués par ses enfants de gauche et de droite (dans l'ordre!), auxquelles s'applique l'opérateur représenté.

struct Noeud {
   Noeud *gauche {},
         *droite {};
   bool feuille() const noexcept {
      return !gauche && !droite;
   }
   //
   // Méthodes abstraite qui seront spécialisées pour les opérateurs et pour les opérandes
   //
   virtual int valeur() const = 0;
   virtual bool est_valide() const = 0;
   Noeud() = default;
   void clear() {
      if (!feuille()) {
         gauche->clear();
         delete gauche;
         gauche = {};
         droite->clear();
         delete droite;
         droite = {};
      }
   }
};
class NoeudValeur : public Noeud {
   int val;
public:
   NoeudValeur(int val) : val{ val } {
   }
   int valeur() const {
      return val;
   }
   bool est_valide() const {
      return feuille();
   }
};
struct NoeudOperateurBinaire : Noeud {
   bool est_valide() const {
      return gauche && droite;
   }
}
struct NoeudSomme : NoeudOperateurBinaire {
   int valeur() const {
      return gauche->valeur + droite->valeur;
   }
};
struct NoeudDifference : NoeudOperateurBinaire {
   int valeur() const {
      return gauche->valeur - droite->valeur;
   }
};
struct NoeudProduit : NoeudOperateurBinaire {
   int valeur() const {
      return gauche->valeur * droite->valeur;
   }
};
class div_par_zero {};
struct NoeudQuotient : NoeudOperateurBinaire {
   int valeur() const {
      auto denom  = droite->valeur;
      if (!denom) throw div_par_zero{};
      return gauche->valeur / denom;
   }
};

Notez que les méthodes requises pour valider chaque Noeud sont implémentées mais n'ont pas été utilisées pour simplifier le propos. Notez aussi que le code requis pour construire un arbre n'a pas été fourni, pour que notre regard demeure porté sur l'essentiel, mais sentez-vous bien à l'aise de rédiger ce code si l'envie vous en prend!

Quelques lectures complémentaires

Si la question vous intéresse, le sujet de la récursivité est vaste, c'est le moins qu'on puisse dire. Vous trouverez ici une courte liste (vraiment rien qui ait la prétention d'être exhaustif!) de lectures complémentaires :

• Programmation récursive, par Edsger W. Dijkstra en 1960 : http://oai.cwi.nl/oai/asset/9253/9253A.pdf
• À propos de la fonction 91 de John McCarthy, qui est une construction récursive quelque peu perverse : http://en.wikipedia.org/wiki/McCarthy_91_function
• En 2011, Michael Fogus émet l'opinion que bien que les langages fonctionnels exigent le recours à la récursivité, ne permettant pas d'avoir recours à des états mutables, il y demeure préférable de procéder par composition de fonctions, la récursivité y étant équivalente à une opération de bas niveau : http://blog.fogus.me/2011/03/09/recursion-is-a-low-level-operation/
• Plusieurs langages fonctionnels implémentent ce qu'on nomme de la Tail Call Optimization, une optimisation transformant de manière systématique un appel récursif en queue de fonction en une forme d'itération. En 2011, Ezra Cooper explique que ce n'est pas un mécanisme si magique que ça, au fond : http://ezrakilty.net/research/2009/11/function_calls_are_not_stack_frames.html
• Chic série de textes sur la récursivité en C++. L'auteur a couvert beaucoup de cas alors si vous souhaitez plus d'exemples, n'hésitez pas :
  • http://www.codeguru.com/cpp/cpp/algorithms/math/article.php/c15111/
  • http://www.codeguru.com/cpp/cpp/algorithms/math/print.php/c15693__4/
  • http://www.codeproject.com/KB/cpp/Recursion_Prmr_CPP_03.aspx
• Pour une autre sorte d'explication de ce qu'est la récursivité, voir ces (courts) textes de John D. Cook :
  • ceci (de 2010) : http://www.johndcook.com/blog/2010/03/30/understanding-recursion/
  • ceci (de 2012) : http://www.johndcook.com/blog/2012/08/14/understanding-recursion-ii/
• À propos de l'importance fondamentale de la récursivité dans la structure de la pensée et des programmes, un texte de Patrick Thomson en 2014 : http://patrickthomson.ghost.io/an-introduction-to-recursion-schemes/
• Texte de 2014 portant sur l'introduction (presque accidentelle) de la récursivité dans les langages de programmation : http://vanemden.wordpress.com/2014/06/18/how-recursion-got-into-programming-a-comedy-of-errors-3/
• Implémenter une forme de Tail Recursion avec des variables 64 bits en C++, texte de Giovanni Campo en 2015 : http://codingadventures.me/2015/03/13/c-tail-recursion-using-64-bit-variables/
• L'histoire secrète (!) de l'avènement de la récursivité en langage C, par Brian W. Kernighan, Dennis M. Ritchie et ... H.P. Lovecraft! http://www.bobhobbs.com/files/kr_lovecraft.html
• Textes de Maarten van Emden :
  • histoire, qualifiée de « comédie d'erreurs », de l'avènement de la récursivité dans les langages de programmation. Texte de 2014 : https://vanemden.wordpress.com/2014/06/18/how-recursion-got-into-programming-a-comedy-of-errors-3/
  • comparer récursivité et itération, texte de 2014 : https://vanemden.wordpress.com/2014/07/30/recursion-versus-iteration/
• Visualiser la récursivité à l'aide de fractals, par Gurkirpal Singh en 2015 : https://singhcodes.wordpress.com/2015/11/08/understanding-recursion-visually-with-fractals/
• Texte pertinent de Robert Harper en 2016, qui rappelle que le concept de pile n'est pas essentiel pour comprendre la récursivité, et qui exprime l'opinion que lier les idées de pile et de récursivité perd au passage la beauté de cette récursivité qui est l'une des plus belles idées du monde de la programmation : https://existentialtype.wordpress.com/2016/02/22/it-is-what-it-is-and-nothing-else/
• Convertir du code récursif en code itératif appuyé d'une pile, par Sai Teja Pratap en 2016 : http://yesteapea.com/2016/04/14/Converting-any-recursion-iteration.html
• En 2016, Jacek Galowicz nous enjoint de ne pas craindre la récursivité : https://blog.galowicz.de/2016/09/11/dont_fear_recursion/
• Texte de 2017 par Eli Bendersky, qui présente la récursivité, la Tail-Recursion, lie les deux à un modèle de programmation par continuations, et discute de trampolines pour fins d'optimisation. Un bon texte, donc : http://eli.thegreenplace.net/2017/on-recursion-continuations-and-trampolines/
• La récursivité exprimée en JavaScript, par Lucas Fernandes Costa en 2017 : http://lucasfcosta.com/2017/05/08/All-About-Recursion-PTC-TCO-and-STC-in-JavaScript.html
• En 2017, texte qui présente la récursivité comme un objet de beauté : http://www.clerro.com/guide/494/the-beautiful-concept-of-recursion
• La récursivité expliquée par Sachin Malothra en 2018 : https://medium.freecodecamp.org/recursion-demystified-99a2105cb871
• Critique de l'enseignement de la récursivité (incluant quelques exemples que vous trouverez ici 🙂) : https://parentheticallyspeaking.org/articles/how-not-to-teach-recursion/
• Je mets rarement des liens vers des vidéos sur mon site, mais celui-ci (qui explique le Tail Call Optimization) est vraiment trop chouette pour laisser passer : https://www.youtube.com/watch?v=-PX0BV9hGZY
• En 2022, Ke Pi distingue récursivité « traditionnelle » et récursivité terminale (Tail Recursion) : https://www.pixelstech.net/article/1474689232-Traditional-recursion-vs-Tail-recursion